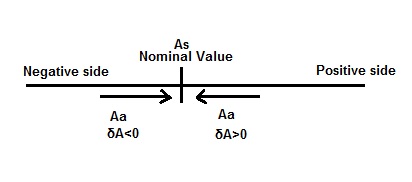
Limiting Error and Relative Limiting Error

Limiting Error is defined as the maximum deviation either in positive side or negative side in the measurement by an instrument from the nominal value or true value. Let us assume that the true value or nominal value of a quantity is A_s and the measured value by the instrument is A_a, then

Limiting Error δA = (Aa – As).

The measured value may be greater than true value As or less than As. Thus δA will be either positive or negative. This is why Limiting Error is specified as ± δA. This error is also known as Guarantee Error as the error in measurement is guaranteed to be within specified limits.

For example, the nominal value of a resistor is 100 Ω with a limiting error of ±10 Ω. The magnitude of measurement will be between the limits, (100±10) Ω i.e. 90 and 110 Ω. Thus the measurement of resistor by the instrument is guaranteed to be between 90 & 110 Ω.

Significance of Limiting Error:

The accuracy of an instrument depends on various factors like material, design and workmanship. Different instrument have different accuracy and hence limiting error. The more the accuracy, the lesser will be the limiting error. But it is not wise to use delicate material and design for every instrument. Actually the selection of instrument depends on the application. For example, if we want to measure the weight of fruits, we won’t need to have weighing machine meant for weighing Gold. This means the selection of an instrument depends on the degree of accuracy required. Thus while choosing an instrument a compromise between the limiting error and degree of accuracy required should be made. Manufacturer generally specifies the limiting error in terms of percentage of rated value of quantity or full scale deviation.

Relative Limiting Error or Fractional Limiting Error:

The Relative or Fractional Limiting error is the ratio of error to the magnitude of nominal value of the quantity. Thus,

Relative Limiting Error ε_r = δA / A_s  ….(1)

Relative Limiting Error is expressed in percentage and hence

% relative limiting error = (δA / A_s)x100

Now from (1),

δA = ε_rA_s  ………(2)

But the actual value or limiting value of measurement,

A_a = As± δA

Hence,

A_a = As± ε_rA_s [from (2)]

     = (1+ε_r)A_s

Let us now consider some examples to better understand relative limiting error.

Example-1:

A 0-150 V voltmeter has a limiting error of 1% of full scale reading. The voltage measured by the instrument is 75 V. Calculate the limiting error in percentage.

Solution: 

The limiting error of voltmeter is 1 % for full scale reading. This means that the error will be (1/100) of 150 = 1.5 V when the voltmeter reads 150 V. As the limiting error of an instrument is same unless mentioned by manufacturer, this means the error in measurement will be 1.5 V for each and every measurement.

Thus when the reading is 75 V, the error will still be 1.5 V. Hence the % limiting error

= (1.5/75)x100 = 2%

Note that the percentage limiting error is twice the mentioned value at full scale reading. The limiting error increases as the reading of voltmeter decrease. If the reading is 37.5 V, the percentage error will be 4%. This increase in error is due to the fact that magnitude of error is constant at 1.5 V irrespective of reading.

So, accuracy at full scale should be chosen if the required reading of quantity in an application is near to the full scale reading of instrument.

Example-2:

A wattmeter having a range of 1000 W has an error of 1% of true value. Find the percentage limiting error when the true power is 100 W.

Solution:

Note here that error is given in terms percentage of true value. This means that the error is not a constant value but it will change as the reading of instrument changes (reading changes as per true power). When the true power is 100 W, the error is 1% of 100 = 1 W. Thus the measured power will be between 99 and 101 W.

Thus if the application requires a wide range to be measured, error in terms of percentage of true value shall be considered.