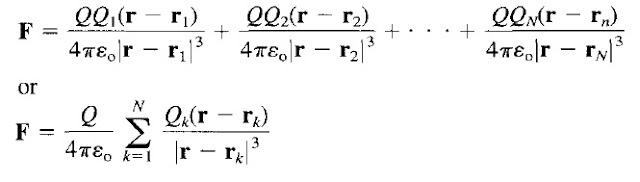Coulomb’s Law

by
Coulomb’s law is an experimental law formulated in 1785 by the French colonel, Charles Augustin de Coulomb. It deals with the force a point charge exerts on another point charge. By a point charge we mean a charge that is located on a body whose dimensions are much smaller than other relevant dimensions. For example, a collection of electric charges on a pinhead may be regarded as a point charge. Charges are generally measured in coulombs (C). One coulomb is approximately equivalent to 6 X 1018 electrons; it is a very large unit of charge because one electron charge e = -1.60 X 10-19 C.

Coulomb’s law states that the force between two point charges Q1 and Q2 is:

a) Along the line joining them

b) Directly proportional to the product Q1Q2 of the charges

c) Inversely proportional to the square of the distance R between them.

Mathematically we can write as below.

F = kQ1Q2/ R2  ……………………(1)

where k is the proportionality constant. In SI units, charges Q1 and Q2are in coulombs (C), the distance R is in meters (m), and the force F is in newtons (N) so that k = 1/4πξ0. The constant so is known as the permittivity of free space (in farads per meter) and has the value

ξ0 = 8.854×10-12= 10-9/ 36π F/m

and k = 1/4πξ0 = 9×109 m/F

Thus from equation (1), we can write as

F = (Q1Q2) / 4πξ0R2 

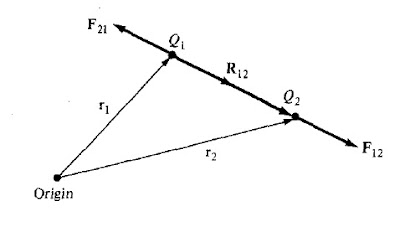
If point charges Q1and Q2 are located at points having position vectors r1 and r2, then the force F12on Q2 due to Q1, shown in figure below, is given by

F12 = [(Q1Q2) / 4πξ0R2] aR12 …………………(2)

Where aR12  is unit vector in the direction of force experienced by charge Q2 by Q1.

Here, R12 = r2– r1 and R is the magnitude of vector R12.

Therefore, unit vector in the direction of R12,

aR12 = R12 / R

Therefore from equation (2), force F12 on Q2due to Q1

F12 = [(Q1Q2) / 4πξ0R2] aR12 

⇒F12 = [(Q1Q2) / 4πξ0R3]R12

      = [(Q1Q2) / 4πξ0R3] (r2 – r1)

Some important points about Coulomb’s Law:

a) It shall be noted that from the figure above that, the force F21, on Q1 due to Q2 is given         by,

F21 = F12aR21 = F12(-aR12)

⇒ F21 = – F12

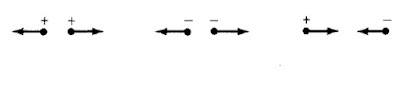
Like charges (charges of the same sign) repel each other while unlike charges attract as shown in figure below.

 
 

b) The distance R between the charged bodies Q1 and Q2 must be large compared with the linear dimensions of the bodies; that is, Q1 and Q2 must be point charges.

c) Q1 and Q2must be static i.e. at rest.

d) If we have more than two point charges, we can use the principle of superposition to determine the force on a particular charge. The principle states that if there are N charges Q1, Q2,……,QN located, respectively, at points with position vectors r1,  r2,. . ., rN then resultant force F on a charge Q located at point r is the vector sum of the forces exerted on Q by each of the charges Q1, Q2,. . ., QN.  Therefore,

Leave a Comment