Difference between Depletion-mode MOSFET and Enhancement-mode MOSFET

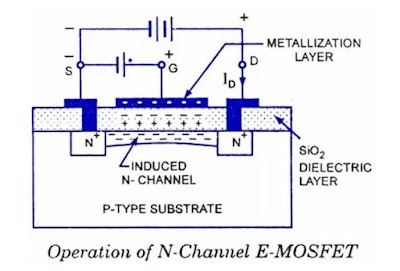
Enhancement Mode MOSFET:

For an enhancement MOSFET, the channel does not initially exist. It only comes into existence once a voltage greater than Vth, threshold voltage is applied. For example, in an n-channel MOSFET, the substrate is made of p-type material. Consider the source to be at a reference ground potential of 0 Volts. For a gate to source voltage of 0 Volts, there is no channel in the p type substrate. Once, the voltage starts to increase, holes are pushed away from the region near the gate due to the increasing positive potential and thus leave behind a region of excess electrons. This region of excess electrons forms the channel for the nMOSFET. That is the reason it is called an n-channel MOSFET.

For a p-channel enhancement MOSFET, since the substrate is of n type, to form a p-type channel, we need to push electrons away from near the gate region which effectively means that we have to apply a negative gate to source voltage/potential. Thus, for an enhancement MOSFET, the channel does not exist at Vgs=0V and comes into play only when the threshold voltage, Vth is exceeded. This is the reason why it is called an Enhancement type MOSFET as the application of a voltage enhances the channel from a state of almost non-existence to a state of existence.

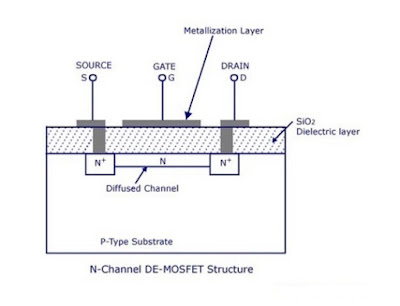
Depletion Mode MOSFET:

For a Depletion type MOSFET, everything is the same except only that the channel is already implanted in the substrate through diffusion. Hence, a current can flow between the source and drain even at Vgs=0 Volt since charge carriers are already present and there is no need to apply a bias voltage to create a region of excess carriers near the gate region.

For example, for the n-channel depletion type MOSFET shown above, the channel has already been implanted into the substrate by diffusion and this is how the device looks without any bias. Compare that to how an enhancement MOSFET looks WITH BIAS as shown in above figure. For the above device, if we start to increase the gate-source voltage, more and more holes will move away from the channel and thus the channel will be deepened, enhanced, as more and more excess uncovered electrons will be left behind by the leaving holes. 

If we now, start decreasing the gate-source voltage, the holes will be attracted towards the gate due to the decreasing potential and thus the channel will start to become more and shallower i.e. depleted. In other words, we can say that the channel is getting Depleted of free carriers i.e. electrons. This is the reason why it is called a Depletion type nMOSFET. It should now become clear that the depletion nMOSFET should have a negative threshold voltage Vth while an n-channel enhancement type MOSFET has a positive threshold voltage.

In short,

Enhancement Mode MOSFET:

Channel doesn’t exist initially. When we apply some input voltage known as threshold voltage channel gets created by repulsion of majority carriers in the bulk region between SOURCE and DRAIN nearby GATE. Default state is OFF i.e. no current flows without applying voltage.

Depletion Mode MOSFET:

Channel already exists. We have to apply some input voltage to collapse the channel so as to stop current flow between SOURCE and DRAIN. Default state is ON i.e. current flows without applying voltage.

Thank you!