Equal Area Criterion is the method of studying the Transient Stability of system of two machines or single machine connected to infinite bus. The study of Transient Stability tells us whether or not synchronism is maintained i.e. whether or not load angle δ settles down to steady state stable value after the clearance of fault or disturbance.
In this post we will focus on
- Equal Area Criterion
- Transient Stability Limit and Margin
- How Transient Stability Margin depend on Breaker Opening time?
- Meaning of Out-of-Step condition in power system
- Meaning of Loss of Synchronism
- Critical Clearing Angle
Concept of Equal Area Criterion:
As we know that under steady state operation of a generator, there exists a balance between the power generation and demand. In other words we can say that mechanical input to generator is balanced with the generated power due to which Generator rotates at a constant synchronous speed. Basically, the output electric power from the generator produces an electric torque that balances the mechanical torque applied to the generator rotor shaft. The generator rotor therefore runs at a constant speed with this balance of electric and mechanical torques. Mind that electromagnetic torque and mechanical torque opposes each other and because of this balance between the mechanical & electromagnetic torque, mechanical energy is converted to electrical energy.
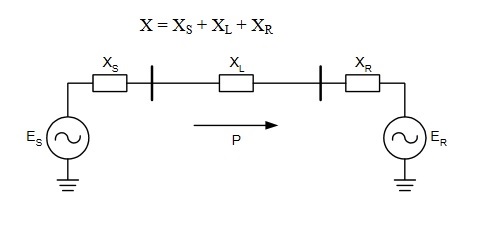
Let us consider a two source system as shown in figure below. The equation of power transfer between the two sources assuming lossless system is given as
P = VsERSinδ / X
Where Vs = Sending end Voltage
VR = Receiving end voltage
X = Transmission Line Reactance + Source Reactance
Thus from the above equation, it is clear that power transfer between the two sources is inversely proportional to the Reactance. If the net reactance increases, power transfer will decrease and vice versa.
During fault condition like Single Line to Ground Fault, Double Line to Ground Fault, Three Phase Fault etc. the effective transmission reactance between the two sources increases depending upon the type of fault. Due to this increase in the effective transmission line Reactance the power transfer between the two sources will reduce. Due to this reduction of power transmission, the electric torque that counters the mechanical torque is also decreased. Thus
Mechanical Torque > Electromagnetic Torque
If the mechanical power is not reduced during the period of the fault, the generator rotor will accelerate with a net input torque (equal to Mechanical Torque – Electromagnetic Torque).
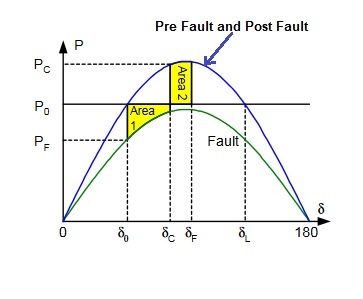
Assume that the two source power system shown in above figure is initially operating at a balance point of δ0 and hence transferring electric power P0. After a fault, the power output is reduced to PF, the generator rotor therefore starts to accelerate, and δ starts to increase. Let’s say the fault is cleared when the angle difference between the sources reaches δC. At this point, fault reactance will not be considered as the system is has attained normal configuration and hence the power transfer will follow the Pre Fault Power Angle Curve as shown in figure below.
But at point δC power output PC is larger than the mechanical power input P0 which will result in deceleration of rotor as
Electromagnetic Torque > Mechanical Torque
However, because of the inertia of the rotor system, the angle does not start to go back to δ0 immediately. Rather, the angle continues to increase till δF such that energy lost during deceleration in Area 2 is equal to the energy gained during acceleration in Area 1. This is called Equal Area Criterion.
Let us consider two cease now for the sake of better understanding of out-of-step condition and application of Equal Area Criterion.
Case-1: If δF < δL or Area 1 < Area 2
Under this condition, the rotor of Generator will oscillate. But because of presence of damping, the amplitude of oscillation will continuously reduce and eventually δ will settle to balanced angle δ0.
Thus we can say that, in this situation the system is Transiently Stable. How much margin we have for transient stability?
If you carefully observe the above Power Angle Curve then you will definitely say that the margin is (δL– δF). Great!
But next question arises, who decides the value of δF?
You must say it is δC i.e. the point of fault clearing. That is why δC is also known as Critical Clearing Angle.
How Transient Stability Margin depends on Breaker Opening Time?
Since the value of δC depends on the point of clearing fault. Therefore, Transient Stability margin i.e. (δL– δF) depends upon the fault clearing time. The less the fault clearing time, less will be the value of δC which means less value of δF. Hence Transient Stability margin will be more. Thus we can say that Transient Stability Margin is dependent on Breaker Opening time to clear the fault. Got it? I guess you get. Please write in comment box.
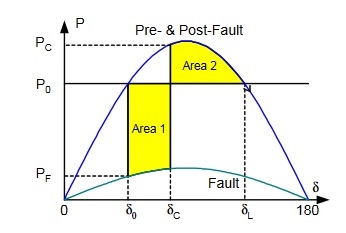
If Area 2 is smaller than Area 1 then at the time the angle reaches δL, then further increase in angle δ will result in an electric power output that is smaller than the mechanical power input. Therefore, the rotor will accelerate again and δ will increase beyond recovery. This is a transiently unstable scenario, as shown in figure above. When an unstable condition exists in the power system, one equivalent generator rotates at a speed that is different from the other equivalent generator of the system. We refer to such an event as a loss of synchronism or an out-of-step condition of the power system.
Please explain Out of step protection Calculation.
It will take time to post on the topics you are suggesting Vishal. But thank you so much for suggesting such a good topics.