First of all we should know why do we need to improve the power factor? Suppose we want to transmit P amount of power to the load center with a power factor of 0.1.
Thus, Current flowing through the Transmission Line I1 = P/0.1V
= 10P/V
It is clear that I2is 10 times lower than the I1. Thus at better power factor the current flowing through the transmission line will reduce which in turn will reduce the I2r loss and increase the efficiency.
Also, a poor power factor at greater load current will lead to poor voltage regulation of Transmission Line, Transformer etc. due to which the performance of Induction Motors, Fluorescent Lamps etc. Thus it is very much important to have power factor close to unity for better utilization of devices, to increase the efficiency and to have a better voltage regulation.
In this way locally the demand of lagging VAR will be met and the supply system will be relieved from supplying the lagging VAR and will only supply active power. As the supply system is only providing the active power and no reactive power,
tanƟ = Reactive Power/Active Power = 0
Hence, Power Factor = CosƟ = Cos0 = 1.
Thus we see using Synchronous Condenser, improves the power factor.
Now, we will take an example to illustrate the thing more clearly.
Example:
A Factory has a total load of 1800 kW at a power factor of 0.6 lagging. If it is desired to improve the power factor to 0.95 using Synchronous Condenser then calculate
- The kVA rating of Synchronous Condenser
- Total kVA of factory.
Solution:
Without installing Synchronous Condenser,
The kVA rating of Factory = 1800 / 0.6 =3000 kVA
Now,
The Reactive Power Demand of Factory = kVAxSinƟ
= 3000×0.8
= 2400 kVAR
Now, we want to improve the power factor to 0.95, hence we need to know how much Reactive Power need to be supplied by Synchronous Condenser.
Reactive Power at a power factor of 0.95,
= kWxtanƟ
= 1800×0.329
= 592.2 kVAR
Mind here that we have used kWxtanƟ not kVAxSinƟ because kW will remain constant but kVA will change when we use Synchronous Condenser.
Thus, the Reactive power which Synchronous Condenser need to supply to improve power factor to 0.95 = (2400 – 592.2) = 1807.8 kVAR
Therefore, the rating of Synchronous Condenser = 1807 kVA as the rating of Synchronous Condenser is in kVA not in kVAR.
Now,
Total kVA rating of Factory =
Here the most important thing to observe that kVA rating of factory has reduced from 3000 to 1894.91 but at the expense of Synchronous Condenser of rating 1807.8 kVA. Thus the current flowing through the cables, transformers etc will reduce and hence will lead to saving in energy bill as the ohmic losses in cable, transformer winding etc. will reduce.
Hope everything is clear now. Thank you!

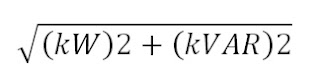

Really Helpful! Thanks a lot!!