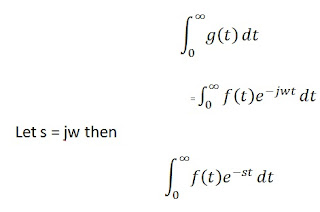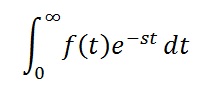In Control System, we often encounter Laplace Transform. Transfer Function is expressed as the ratio of Laplace Transform of output and input to a system. Laplace Transform is used to ease the calculation as solving differential equation is quite tiresome. Suppose there is a second order differential equation, then solving of the second order differential equation will be very tiresome but if we convert this differential equation into Laplace Transform then it will reduce to a quadratic equation which is easy to solve. Laplace Transform converts the time domain function f(t) is into frequency domain.
Origin of Laplace Transform
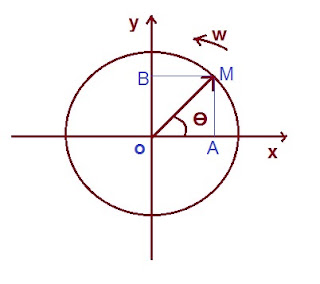
Let us consider a time domain function e-jwt .
e-jwt = Coswt + jSinwt
The magnitude of this function is obviously UNITY. But the important feature of this function is that it is a rotating vector in anticlockwise direction with angular speed w as shown in figure below.
The vector OM can be divided into two component, one along the X axis and another along the Y axis. Thus we can write
OM = OMCosƟ + j(OM)SinƟ where Ɵ = wt
But the magnitude of OM = 1, hence
OM = CosƟ + jSinƟ = Coswt + jSinwt
= e-jwt
Therefore if we multiply any time domain function f(t) by e-jwt, the magnitude of f(t) is not going to change. But the function is changed from time domain to frequency domain. Well, now how to find the aggregate value of this function?
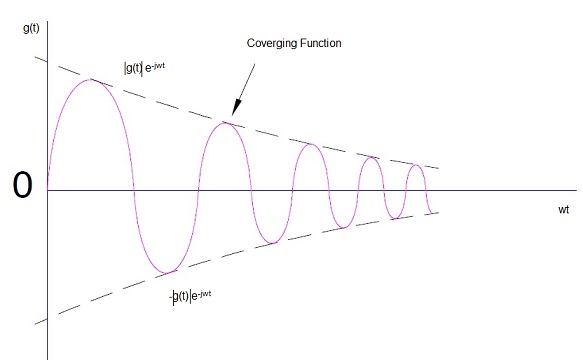
To get the answer, we consider a function g(t) = e-jwt Sinwt. The maximum and minimum value of g(t) are e-jwt and – e-jwt respectively. Therefore the graph of g(t) will be as shown below.
From the above graph we can see that the value of function when time tends to infinite is zero. This means that the function gets converges. Therefore whenever function is multiplied by e-jw it becomes converging in nature. Therefore to find the aggregate value of g(t) over the whole time domain i.e. zero to infinity, we can use integration as below.
Isn’t the above integration Laplace Transform of function f(t)??? Hehehe….Yes it is. Thus Laplace Transform of function f(t) for t >=0 is denoted as L[f(t)] and defined as
Hope you enjoyed. Thank you!