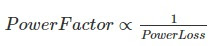As we know that power factor is the ratio of the actual power being consumed by an appliance to the apparent power it draws from the source.
Things get a little weird when we connect inductive/capacitive devices to an AC source. The inductive or capacitive devices don’t actually utilize any power, instead in one half of the cycle, they store the energy in magnetic and electrical fields formed around them respectively, while in the other half, they release that stored energy. So, we might think that if the stored energy is released in that very circuit, there should be no power losses. However, laws of thermodynamics state that conversion of energy into another form always takes place with loss of some part of that energy, which can vary according to the efficiency of the device. This means that energy is perpetually lost between conversion, which gives rise to the power losses in case of LR / CR circuits.
Now, how the two are related. Mathematically, power factor is equal to the cosine of the base angle in an impedance triangle:
Greater the inductive/capacitive reactance, lesser is the power factor and consequently is a greater apparent load as compared to the actual load. Notice that power factor is the ratio of Resistance/Impedance, that multiply the two by I2, and we have
Now, this means that as the power factor decreases, the amount of energy being spent in the resistor decreases. Now since inductors and capacitors act only as energy reservoirs with low efficiency, power losses increase significantly as power factor of a circuit decreases.
Therefore,