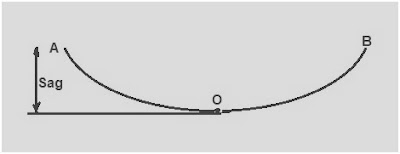
Sag in overhead Transmission line conductor refers to the difference in level between the point of support and the lowest point on the conductor.
Sag in Transmission line is very important. While erecting an overhead Transmission Line, it should be taken care that conductors are under safe tension. If the conductors are too much stretched between two points of different Towers to save conductor material, then it may happen so that the tension is conductor reaches unsafe value which will result conductor to break.
Therefore, in order to have safe tension in the conductor, they are not fully stretched rather a sufficient dip or Sag is provided. The dip or Sag in Transmission line is so provided to maintain tension in the conductor within the safe value in case of variation in tension in the conductor because of seasonal variation. Some very basic but important aspects regarding Sag are as follows:
1) As shown in the figure above, if the point of support of conductor is at same level from the ground, the shape of Sag is Catenary. Now we consider a case where the point of support of conductor are at same level but the Sag is very less when compared with the span of conductor. Here span means the horizontal distance between the points of support. In such case, the Sag-span curve is parabolic in nature.
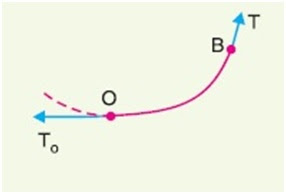
2) The tension at any point on the conductor acts tangentially as shown in figure above. Thus the tension at the lowest point of the conductor acts horizontally while at any other point we need to resolve the tangential tension into vertical and horizontal component for analysis purpose. The horizontal component of tension remains constant throughout the span of conductor.
Calculation of Sag:
As discussed earlier in this post, enough Sag shall be provided in overhead transmission line to keep the tension within the safe limit. The tension is generally decided by many factors like wind speed, ice loading, temperature variations etc. Normally the tension in conductor is kept one half of the ultimate tensile strength of the conductor and therefore safety factor for the conductor is 2.
Now, we will calculate the Sag in an overhead transmission line for two cases.
Case1: When the conductor supports are at equal level.
Let us consider an overhead line supported at two different towers which are at same level from ground. The point of support are A and B as shown in figure below. O in the figure shows the lowest point on the conductor. This lowest point O lies in between the two towers i.e. point O bisects the span equally.
Let,
L = Horizontal distance between the towers i.e. Span
W = Weight per unit length of conductor
T = Tension in the conductor
Let us take any point P on the conductor. Assuming O as origin, the coordinate of point P will be (x,y).
Therefore, weight of section OP = Wx acting at distance of x/2 from origin O.
As this section OP is in equilibrium, hence net torque w.r.t point P shall be zero.
Torque due to Tension T = Torque due to weight Wx
Ty = Wx(x/2)
Therefore, y = Wx2 / 2T ……………………….(1)
For getting Sag, put x = L/2 in equation (1)
Sag = WL2/8T
Case2: When the conductor supports are at unequal level.
In hilly area, the supports for overhead transmission line conductor do not remain at the same level. Figure below shows a conductor supported between two points A and B which are at different level. The lowest point on the conductor is O.
Let,
L = Horizontal distance between the towers i.e. Span
H = Difference in level between the two supports
T = Tension in the conductor
X1 = Horizontal distance of point O from support A
X2 = Horizontal distance of point O from support B
W = Weight per unit length of conductor
From equation (1),
Sag S1 = WX12/2T
and Sag S2 = WX22/2T
Now,
S1 – S2 = (W/2T)[ X12 – X22]
= (W/2T)(X1 – X2)( X1 + X2)
But X1 + X2 = L …………………….(2)
So,
S1 – S2 = (WL/2T)(X1 – X2)
X1 – X2 = 2(S1 – S2)T / WL
X1 – X2 = 2HT / WL (As S1 – S2 = H)
X1 – X2 = 2HT / WL ………………..(3)
Solving equation (2) and (3) we get,
X1 = L/2 – TH/WL
X2 = L/2 + TH/WL
By putting the value of X1 and X2 in Sag equation, we can easily find the value of S1 and S2.
The above equations for Sag are only valid in ideal situation. Ideal situation refers to a condition when no wind is flowing and there is no any effect of ice loading. But in actual practise, there always exists a wind pressure on the conductor and as far as the ice loading is concerned, it is mostly observed in cold countries. In a country like India, ice loading on transmission line is rarely observed.
Effect of Wind and Ice Loading on Sag:
Coating of ice on conductor (it is assumed that ice coating is uniformly distributed on the surface of conductor) increases the weigh of the conductor which acts in vertically downward direction. But the wind exerts a pressure on the conductor surface which is considered horizontal for the sake of calculation.
As shown in figure above, net weight acting vertically downward is sum of weight of ice and weight of conductor.
Therefore,
Here,
W = Weight of conductor per unit length
Wi = Weight of ice per unit length
Ww = Wind force per unit length
= Wind PressurexArea
= Wind Presuurex(2d+t)x1
Note the way of calculation of Area of conductor. What I did, I just stretched the conductor along the diameter to make a rectangle as shown in figure below.
Thus from equation (1),
Sag = WtL2/2T
and the angle made by conductor from vertical = tanƟ
= Ww / (W+Wi)

I admire your work and calculations done on sagging transmission lines.Thank you I appreciate this so much, always notify me on your page.
Thank you Frank. For getting notification, please press the bell icon. Please like and share my facebook page Electrical Concepts
All my concepts are clear now. Though my exam is tomorrow, but the way calculation is done, I can slove any problem now!
Thank you so much!
😇📕📓
Thank you , your notes are brief and clear! Really liked it
This was interesting keep it up
It is interesting and clears fundaments of Sag.
Also, include one practical example of 220KV line by giving the value of span, conductor weight, tension, etc.
How would you calculate the tension? The formula above mentioned is for kids where tension is given on the basis of temperature. If there is no incorporation of temperature, you can’t apply the formula to calculate sag in real life.
What is the allowable limit for sag?
Fond memories. One of the first computer programs I worked on (1967) was Sag & Tension. We obtained the FORTRAN program from Cincinnati Gas& Electric and my task was to get it running on our in house computers. I worked in the Engineering Division of P&G. Prior to getting this program, we had a Russian émigré contractor who did the calculations on a slide rule using printed function tables! As I recall, it took a couple of days for him to do the calculations.
Wow…thank you very much for sharing your experience. Keep adding value
There is a minor mistake.
S2-S1 = H
Not S1-S2=H
There seems to be a mistake because the conductor weight of section OP is not equal to Wx, because the conductor length between O and P is longer than x or do I miss something?