Strain Gauge is basically a sensor used for the measurement of various physical parameters like stress, strain etc. The working principle of strain gauge is based on Piezoresistive Effect. This is why it is also often called Pizoresistive Gauge.
When a metal conductor is stretched or compressed, the dimension of conductor changes. Change in dimension means change in radius and length of the conductor. Since the resistance of conductor is directly proportional to its length and inversely proportional to its area of cross-section, therefore a change in dimension of conductor will cause a change in the resistance. Also, it has been observed that the resistivity of conductor also changes due to strain in the conductor. This change in resistivity of due to strain is called Piezoresistive Effect.
Principle of Strain Gauge:
Let us consider a conductor of length L and diameter D. This conductor is now stretched by force F as shown in figure below.
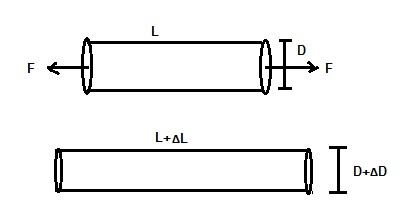
Due to this applied force F, there will be a change in longitudinal and lateral dimension. The length changes to L+ ΔL and diameter changes to D+ ΔD. It is obvious that in case of positive strain i.e. when conductor is stretched, there will be a reduction in diameter whereas increase in length. Hence the resistance will increase as per the formula given below.
R = ρL/A …………….(1)
Where ρ = resistivity
A = Cross-sectional area
L = Length
But it has been observed experimentally that the increase in resistance of conductor is more than the calculated value from equation (1). This extra increase in resistance is attributed to the slight increase in resistivity of the conductor due to Piezoresistive Effect.
Being a transducer, this physical change in dimension is converted in electrical parameter i.e. resistance which is easily measured. Thus Strain Gauge converts stress / strain into resistance.
Gauge Factor:
Gauge Factor is defined as the ratio of per unit change in resistance to the per unit change in length. This can be mathematically written as,
Gf = (ΔR / R) / (ΔL / L)
Where
ΔR / R = Per unit change in resistance
ΔL / L = Per unit change in length
Gf = Gauge Factor
As strain of an elastic material is defined as the per unit change in length, therefore
Strain, ε = Change in Length / Original Length
= ΔL / L
Hence,
Gauge Factor, Gf = ε(ΔR / R)