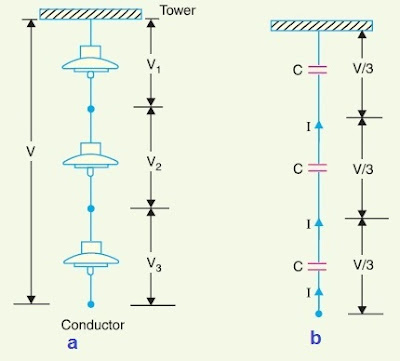
A Suspension Insulator is basically a string of number of porcelain disc connected in series though metallic link. It shall be noted that the number of discs in Suspension Insulator can be increased or decreased by adding extra discs or removing a disc. Figure-a below shows a typical Suspension Insulator.
As discussed in above paragraph, porcelain disc remain in between the metallic links, therefore each disc acts as a Capacitor. Therefore, if we draw the equivalent circuit for a suspension insulator, it will be as shown in figure-b.
Thus when such type of insulator is connected to hold a power conductor carrying electrical power at high voltage, a charging current will flow though the series connected Capacitors. As the charging current through each of the Capacitor (Porcelain disc) is same, therefore the potential distribution across each Porcelain disc will be same i.e. each Porcelain disc will have equal voltage stress. Let us assume that the voltage at which power conductor carrying electrical power be V, then for suspension insulator, potential across each Capacitor i.e. Porcelain disc will be V/3.
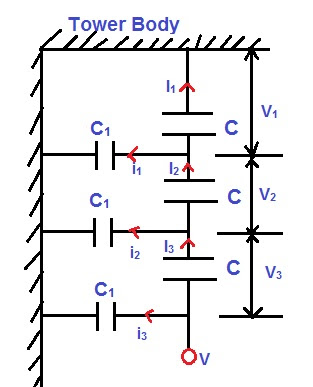
As can be seen from the figure above,
I3 > I2 > I1
Therefore, V3 > V2 > V1
Though each disc is designed to withstand same voltage stress, say 11 kV, but the disc nearer to the power conductor is much stressed, say 16 kV, while the disc farther from the conductor is less stressed. Thus proper utilization of disc is not achieved due to shunt capacitance. Some discs are underutilized while disc nearer to conductor is over utilized which may lead to damage of the disc. Thus a term called String Efficiency originates from this philosophy.
String Efficiency of Suspension Insulator String:
String Efficiency shows the utilization of suspension insulator. More the utilization of discs of insulator more will be the string efficiency.
String Efficiency is defined as the ration of conductor voltage and the voltage across the disc nearest to conductor multiplied by number of discs.
Thus,
String Efficiency = Conductor Voltage / (nxvoltage across the disc nearest to conductor)
n = Number of discs in suspension insulator.
Here comes the Grading Ring or Guard Ring. Grading Ring or guard Ring equalizes the potential distribution across each disc in Suspension Insulator. Thus if the voltage across each disc becomes equal then String Efficiency will be 100%.
Shall we calculate String Efficiency and voltage distribution in string insulator? No….But still I will show you the calculation, please give me your extra 10 minutes.
Calculation of Voltage Distribution:
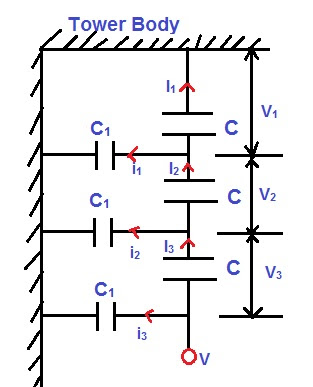
C1 = Shunt Capacitance
C = Self Capacitance
Let us assume that C1= KC, where K is some constant.
As obvious from the figure above,
I2 = I1+i1
⇒V2wC = V1wC + V1wC1
⇒ V2wC = V1wC + V1wKC
⇒ V2 = V1(1+K) ………………….(1)
Similarly,
I3 = I2+ i2
⇒ V3wC = V2wC + (V1 + V2)wC1
⇒ V3wC = V2wC + (V1 + V2)wKC
⇒ V3= V2 + (V1 + V2) K
Putting the value of V2from equation (1),
= V2 + (V1 + V2)K
= KV1 + V2(1 + K)
= KV1 + V1(1+K)2 ………….[from equation (1)]
= V1[1+3K + K2]
Thus,
V3= V1[1+3K + K2] ……………..(2)
Now,
Voltage between conductor and earth V,
= V1 + V2+ V3
Putting the value of V2 and V3 from (1) and (2),
= V1[3 + 4K + K2]
= V1(1+K)(1+3K)
So,
V = V1(1+K)(1+3K) ………………….(3)
Therefore,
V1 = V / (1+K)(1+3K)
V2 = V1(1+K)
V3 = V1(1+3K+K2)
Also,
String Efficiency = (Vx100) / (3xV3) %
From the above expression of V1, V2 and V3, we observe that more the value of K, more non uniform is the potential distribution across the discs and hence less is the efficiency of string.
Also, as the number of discs increases in the suspension insulator, the inequality in voltage distribution increases. Thus shorter string has more efficiency than larger string.
What is w in VwC
w is omega and
VwC is current
V=IXc
Xc=1/wC
I=VwC
w is omega i.e. angular frequency.
How to find out the number of insulator disc in suspension type string ????
by the help of following formula
line voltage/(3)^1/2x 11
because in the line always line voltage so have to convert it into the phase voltage then it divide by 11 because each disc is made for 11 kv rating.
Mitesh Kavar, generally one disc can withstand a voltage stress of 11 kV. So the number of disc can be roughly calculated by dividing the phase voltage level by 11.
I have seen 11 or 10 discs on 132 kv side. What is the reason?
Practically gaurd ring distribute uniformly voltage at only 4-5 disc so other disc not share full rated KV hence we use some extra disc for improving FOS(factor of sefty)
Thank you Vijay for value addition.
How to calculate string efficiency for more than three insulators
The same philosophy of calculation of string efficiency applies for n number of insulators.
How to calculate string efficiency for more than three insulators?
i.e for 4 insulator discs
The method will be same. I fact the method can be applied for n number of insulators.