Surge Impedance is the characteristic impedance of a lossless transmission line. It is also called Natural Impedance because this impedance has nothing to do with load impedance. Since line is assumed to be lossless, this means that series resistance and shunt conductance is negligible i.e. zero for power lines.
This means that, Series Resistance R = 0 and Shunt Conductance G = 0
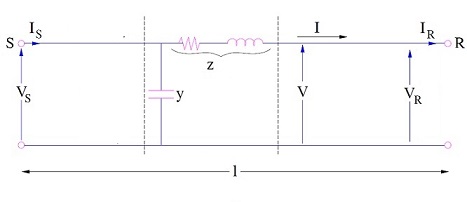
As Characteristic Impedance Zc = z/y
where z is series impedance per unit length per phase and y is shunt admittance per unit length per phase.
z = R +jwL
y = G + jwC
For lossless line, z = jwL and y = jwC
Hence according to definition,
Surge Impedance = Zs = Zc = √(jwL/jwC)
= √(L/C)
Surge Impedance Loading SIL
A transmission line terminated with load equal to surge impedance of line is called surge impedance loading SIL.
Let us a look at the voltage profile along the line for surge impedance loading condition. We know that voltage at any point is given as
V = [(Vr +ZcIr)/2]eµx + [(Vr-ZcIr)/2]e-µx
Where Zc is characteristic impedance. Since line is assumed lossless therefore characteristic impedance and surge impedance will be equal i.e. Zc = Zs. Also, line is terminated with surge impedance therefore Vr = ZsIr
V = [(Vr +ZsIr)/2]eµx + [(Vr-ZsIr)/2]e-µx
= ZsIr eµx
Since µ = √yz = µ = √(j2w2LC) = jw√LC
V = ZsIr ejwx√LC
Assuming wx√LC = Ɵ
V = ZsIr ejƟ = ZsIr ∠Ɵ
The above expression of voltage shows that, for surge impedance loading the voltage profile along the line is uniform or flat. This means sending end voltage and receiving end voltages are same for surge impedance loading.
Thus SIL can also be defined as,
Surge Impedance Loading is the connected load in transmission line for which reactive power generated is equal to reactive power consumed i.e. the flow of reactive power is zero. There is an exact balance between reactive power generation and consumption. Mind that reactive power is generated here by shunt capacitance and being consumed by series inductance of line.
From the above definition of SIL, we can have a second method to calculate Surge Impedance Zs.
Reactive Power Generated = Reactive Power Consumed
V2wC = I2wL
(V/I) = √(L/C)
Zs = √(L/C)
|
Surge Impedance Zs = √(L/C)
|
Hope you fully understand the concept. Still if you have any doubts please comment. Thank you!
Thank you ..nicely explained
Thank you Abhinav!
Why we have to study about surge impedance and loading..?can u explain one example please…thank u