VVVF stands for Variable Voltage Variable Frequency. VVVF Speed Control method is widely used method for Induction Motor.
Origin of VVVF Speed Control
As we know that synchronous speed of machine is given as
N (rpm) = 120f/P …………………………………(1)
where f is frequency and P is number of pole.
Thus if we can change the frequency f then it is possible to change the speed of induction motor. Now frequency of power supply can easily be varied using power electronics devices like inverter. The inverter converts DC power into AC power and feeds to induction motor. Inverter output may be either constant voltage variable frequency or variable voltage variable frequency. Which one to choose?
Suppose inverter output is constant voltage but variable frequency.
Thus we can write V = Constant but f = Variable.
The relationship between voltage V and frequency f is well known and can be written as
V = 4.44fNØ ……………………………….(2)
where N is number of turns per phase and Ø is resultant air gap flux.
Suppose we want to reduce the speed of induction motor. For this, obviously we will have to reduce the frequency f while keeping V constant as per (1). But from (2),
Ø = V / (4.44fN) …………………………..(3)
Air gap flux Ø will increase which may cause machine core to saturate which is not desirable. Thus the concept of speed control with constant voltage variable frequency cannot be adopted.
But from (3), it is possible to achieve constant flux Ø by maintaining (V/f) constant. This allows us to change voltage and frequency simultaneously to have speed control while maintaining constant air gap flux. This is the basic concept behind VVVF speed control of induction motor.
Torque in VVVF Speed Control
As discussed, frequency is varied, therefore it is quite important to have a look at the maximum torque at variable frequency. Refer the equivalent circuit of Induction Motor.
As we know that torque in an induction motor is given as
T = [k2f2 / (R2/s)2+(ωL2)2]x(R2/sω)
To get the maximum torque, we need to differentiate the above equation w.r.t s and equate it to zero. This will give us the value of slip s’ at which torque is maximum as below.
s’ = (R2/ωL2) ……………..(4)
Therefore, maximum torque Tmax = k2/8π2L2
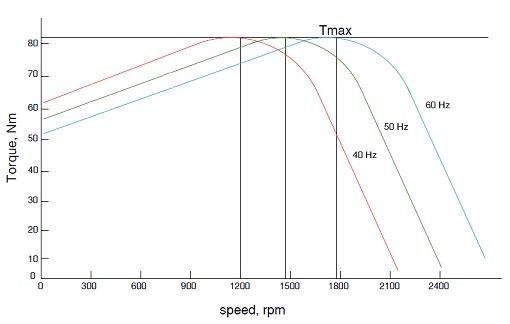
Thus maximum torque is independent of frequency. But the speed at which maximum torque will appear will vary slightly as per (4). Refer the figure below.
As we increase the frequency f, ω = 2πf also increases. This in turn will reduce s’ as per (4). Thus increasing the frequency will increase the speed of induction motor and speed at which maximum torque appears while having the same maximum torque.

Very good explanation