2’s complement subtraction method is a way to subtract two binary numbers by actually adding one number with the 2’s complement of another number. In this article, the method of binary subtraction using 2’s complement is elaborated with examples.
Method of 2’s Complement Subtraction:
To implement this method for subtracting two binary numbers, the very first step is find the 2’s complement of the number which is to be subtracted from another number. To get the 2’s complement, first of all 1’s complement is find and then 1 is added to this. The addition is the required 2’s complement.
Suppose, we need to find the 2’s complement of binary number 10010. First, find 1’s complement. To find this, replace all 1 to 0 and all 0 to 1. Therefore, 1’s complement of 10010 will be 01101. Now, add 1 to this as shown below.
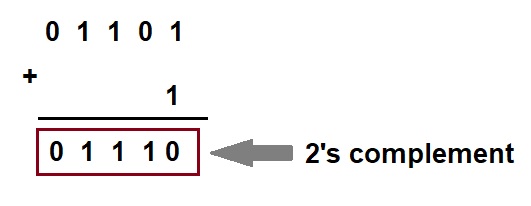
Steps for 2’s Complement Subtraction:
Subtraction of Smaller Number from Larger Number:
To subtract a smaller number from a larger number using 2’s complement subtraction, following steps are to be followed:
Step-1: Determine the 2’s complement of the smaller number
Step-2: Add this to the larger number.
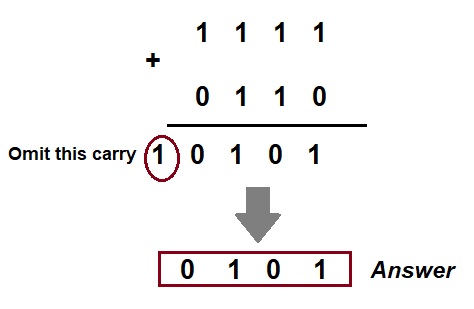
Step-3: Omit the carry. Note that, there is always a carry in this case.
Following example illustrate the above mentioned steps:
Exampe-1: Subtract (1010)2 from (1111)2 using 2’s complement method.
Solution:
Step-1: 2’s complement of (1010)2 is (0110)2.
Step-2: Add (0110)2 to (1111)2. This is shown below.
Subtraction of Larger Number from Smaller Number:
To subtract a larger number from a smaller number using 2’s complement subtraction, following steps are to be followed:
Step-1: Determine the 2’s complement of the smaller number
Step-2: Add this to the larger number.
Step-3: There is no carry in this case. The result is in 2’s complement form and is negative.
Step-4: To get answer in true form, take 2’s complement and change its sign.
Following example will definitely help you to understand the above steps:
Example-2: Subtract (1010)2 from (1000)2 using 2’s complement.
Solution:
Step-1: Find the 2’s complement of (1010)2. It is (0110)2.
Step-2: Add (0110)2 to (1000)2.
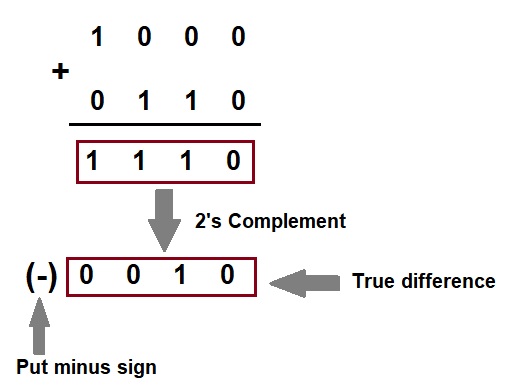
Step-3 and Step-4 has been explained in the above difference calculation.
Advantages:
Though both 1’s and 2’s complement method for subtracting binary numbers seems to be complicated when compared with direct method of subtraction of two binary numbers, both have some distinct advantage when applied using logic circuits, because they allow subtraction to be done using only addition. The ‘s and 2’s complement of a binary number can easily be arrived at using logic circuits; the advantage in 2’s complement subtraction is that the end-around-carry operation present in 1’s complement method is not involved here.
Perform (147-89) using 2’s complement binary arithmetic
hello,i hope you are fine .My question i Perform Binary Subtraction for (102)10 – (201)10 i get answer is -99 how i convert -99 to +99