1’s complement subtraction is a method to subtract two binary numbers. This method allows subtraction of two binary numbers by addition. The 1’s complement of a binary number can be obtained by replacing all 0 to 1 and all 1 to 0. This article discusses steps involved in 1’s complement subtraction of a smaller number from a larger number & the steps for subtracting a smaller number from a larger number with example.
Steps for 1’s Complement Subtraction:
Subtraction of Smaller Number from Larger Number:
The steps for 1’s complement subtraction of a smaller number from a larger binary number are as follows:
Step-1: Determine the 1’s complement of the smaller number.
Step-2: Add this to the larger number.
Step-3: Remove the carry and add it to the result. This carry is called end-around-carry.
Following examples illustrates the septs involved in 1’s complement subtraction of a smaller number from larger number.
Example-1: Subtract (1010)2 from (1111)2 using 1’s complement method.
Step-1: Find the 1’s complement of 1010. It will be found by replacing all 0 to 1 and all 1 to 0. In this way, the required 1’s complement will be 0101.
Step-2: In this step, we need to add the vale calculated in step-1 to 1111. This is shown below.
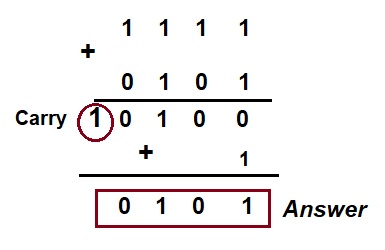
For your reference, addition of binary digits 1 + 1 = 10. Also, note that carry 1 has been added to the addition to get the subtraction of the binary numbers. Thus, the subtraction is done by actually adding two binary numbers.
Subtraction of Larger Number from Smaller Number:
The steps involved in 1’s complement subtraction of a larger number from a smaller number are as follows:
Step-1: Determine the 1’s complement of the larger number.
Step-2: Add this to the smaller number.
Step-3: The answer is the 1’s complement of the true result and opposite in sign. There is no carry.
Following examples illustrates the application of above mentioned septs for subtraction of a larger number from smaller number.
Example: Subtract (1010)2 from (1000)2 using 1’s complement method.
The 1’s complement of (1010)2 is (0101)2. Now, we will add this with the smaller number and finally take 1’s complement of the result to get the answer. This is shown below.

Mind that, no carry has been obtained while subtracting a larger number from a smaller number. Further, a minus sign has been put.
Hey, great post! I must say you have provided us with such useful and productive content. Keep posting!!
is the minus sign at the end only applicable if there is a 1 in the most significant bit?
Waaw what else should I say, its been a helpful article keep posting
Waw what else should I say, its been a helpful article, keep posting
Thank you!