GMD & GMR stands for Geometrical Mean Distance and Geometrical Mean Radius. This concept is very useful in Power System for the calculation of Inductance and Capacitance of Transmission Line.
Basically, as we know that Geometrical Mean of n numbers a1,a2,a3,….,anis
(a1a2a3a4….an)1/n
The same concept is also used for the calculation of GMD and GMR. In GMD we take the Geometrical Mean of distances between the strands of two Transmission Lines while in GMR, Geometrical Mean of distances between the stands of a single composite conductor are calculated.
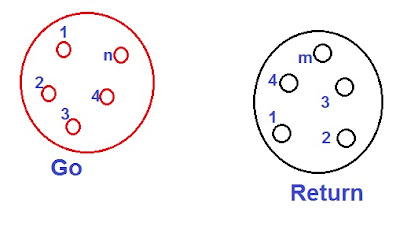
Let us assume two composite conductors used in Transmission Line as shown in figure below.
As shown in the figure above, one conductor is Go and another is Return for current for single phase line. The current is assumed to be equally divided among all the strands of a conductor.
Therefore,
Current carried by each strand in Go conductor = I/n
Current carried by each strand in Return conductor = -I/m
Here I is the total current carried by each conductor.
Now, we will calculate the GMD and GMR for the configuration of the conductors shown in figure above.
For getting the GMD, first we need to calculate the distance between the strands of Go and Return conductors.
Let,
D11 = Distance between the 1ststrand of Go and Return conductor
D12 = Distance between the 1ststrand of Go and 2nd strand of Return conductor
D21 = Distance between the 2nd strand of Go and 1st strand of Return conductor
Dmn = Distance between the mthstrand of Go and nth strand of Return conductor
Geometrical Mean Radius of a solid conductor or a strand of radius R is defined as the factious radius R’ having no internal flux linkage but having the same inductance as the original conductor of radius R.
R ‘ = 0.7788R
For calculating GMR, first we find the distance between the individual strands. Thus if there are n strands in a composite conductor then obviously there will be n2 distances between the strands.
Let us now consider an example to make our concept clear. As shown in figure below, go conductor contain three strands of radius 2.5 mm while the return conductor contains two of radius 5mm.
GMR of individual strands in Go conductor R’ = 0.7788xR
= 0.7788×2.5
= 1.947mm
GMR of Go Conductor
= [(1.947x6x12)(1.947x6x6)(1.947x6x12)]1/9
= 0.4809m
Similarly,
GMR of individual strands in Return conductor R’ = 0.7788xR
= 0.7788×5 mm
= 0.003894 m
Hence, GMR of Return Conductor
= [(0.003894×6)(0.003894×6)]1/4
= 0.1528 m
Now, distance between strand a and e Dae = [92+62]1/2
= 10.81 m
Distance between strand c and d, Dcd = [92+122]1/2
= 15 m
Therefore,
GMD for the configuration,
= [9×10.81×10.81x9x15x10.81]1/6
= 10.74 m



awesome explanation with numerical.. thnx.
thank you!
radius is in mm and distance is in m and u have solved it without unit conversion
This much unit conversion you can do dear. Once unit conversion has been done, carefully see. Thank you very much next time I will do this much of unit conversion.
This much unit conversion you can do dear. Once unit conversion has been done, carefully see. Thank you very much next time I will do this much of unit conversion.
Thank u so much good and easy exppanations
From where u got R'=0.778R?
Please read Geometrical Mean Radius (GMR) and Inductance to know why R'=0.7788R.
Thank you clear explanation
thank you perfect explanation
Thanks alot ,it really helped 😊