Geometrical Mean Radius (GMR) and Inductance

Geometrical Mean Radius GMR is basically the Geometric Mean of distances between the strands of a conductor. It is the fictitious radius of conductor having no internal flux linkage but only external flux linkage. To understand the concept of GMR and its calculation, it is very important to understand the calculation of inductance of Single Phase Two Wire Line.

Inductance of Single Phase Two Wire Line

A single phase two wire system consists of two conductors, one is phase and another one is neutral conductor. Though in AC system, concept of GO and RETURN current does not exist but we can always analyze using RMS value of currents. Hence phase conductor can be assumed to be GO conductor and Neutral conductor as RETURN conductor. Here GO means current is going to the load through phase and RETURN means current is returning back to the source through Neutral conductor. Obviously the value of current in GO and RETURN conductor is same but their direction is opposite.

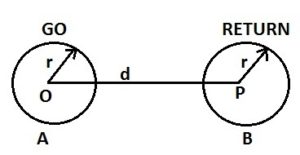
The two conductors of Single Phase Two wire line forms a current loop. This current loop will produce a magnetic field in its surrounding which will link with the conductors. Due to this flux linking, there will be certain amount of inductance of the conductors. We are about to calculate this inductance.

The above figure shows the two conductors separated by a distance ‘d’ and carrying current I. The inductance of both the conductors will be equal due to symmetric arrangement. Therefore we will only calculate inductance of conductor A.

Conductor A will link with its own internal flux as well as external flux from the surface of conductor to ‘d’. We know that internal flux linkage of a single conductor is given as

Ø_int = µI/8π

Now, magnetic filed intensity at any point is given as

H = I/2πx AT/m

Therefore magnetic flux density at any point (assuming permeability of medium to be µ) is given as

B = µH

   = µI/2πx

Hence, the external flux linkage of conductor A,

                                          

                                          

Hence, total flux linkage of conductor A

ψ = µI/8π + (µI/2π)log(d/r)

   = (µI/2π)[1/4 + log(d/r)]  ……….(2)

The above expression represents the total flux linkage of conductor A. Therefore as per the definition of Inductance,

L_A = Inductance of conductor A

     = ψ / I

     = (µ/2π)[1/4 + log(d/r)]

Assuming the medium between the conductors A and B to be air,

µ= µ₀ = 4πx10^-7

Hence, Inductance L_A of Conductor A,

L_A = 2πx10^-7[1/4 + log(d/r)]

As mentioned earlier in the post, due to symmetry the inductance of conductor A and B will be same, hence

L_B = 2πx10^-7[1/4 + log(d/r)]

Carefully observe the above expression of inductance. You will notice that it is having two components. The first component is due to internal flux linkage of conductor and the second term is due to external flux linkage. Generally analysis of effect of surrounding conductors on a single conductor in transmission system is carried out. Therefore the effect of internal flux linkage on a single conductor is accounted by taking Geometrical Mean Radius GMR of single conductor instead of ‘r’. This permit us to only consider external flux for study of inductance.

The Geometrical Mean Radius GMR of conductor is taken in such a way that inductance of conductor due to external flux linking becomes equal to the original inductance L_A. This means

(µ/2π)log(d/GMR) = (µ/2π)[1/4 + log(d/r)] 

log(d/GMR) = 1/4 + log(d/r)

                   = log_e(e^1/4) + log(d/r)

                   = log[e^1/4x(d/r)]

                   = log[d / (e^-1/4xr)]

GMR = e^-1/4xr = 0.7788r

Thus Geometric Mean Radius GMR of a conductor is that fictitious radius which do not has any internal flux linkage but only have external flux linkage. GMR of a conductor of radius r is given as

GMR = 0.7788r

Therefore, inductance of conductor of single phase two wire line in terms of Geometrical Mean Radius, GMR is given as

L = 2πx10^-7log(d/GMR)