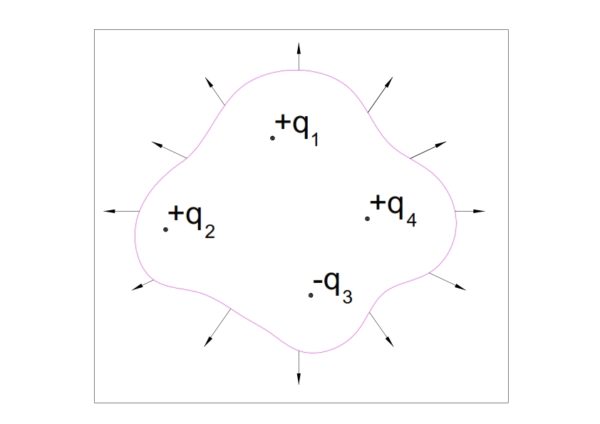
Gauss Law states that, the flux of net Electric Field through a closed surface is equal to the net charge enclosed by the closed surface divided by permitivity of space.
Therefore, mathematically it can be written as
∫E.ds = Qint/ξ (Integration is done over the entire surface.)
where Qint = Total charge enclosed by the close surface
and ξ = permitivity of space = ξ0ξr
Let us consider a closed surface as shown in figure below and apply Gauss Law.
The direction of Electric Field through the closed surface is shown in figure. The flux of net electric field through the closed surface
∫E.ds = (q1+q2+q4-q3) / ξ
It shall be noted here that while applying Gauss Law, the electric field considered through the surface shall be the net electric field due to both the charges inside and outside the closed surface. But the Qint shall only account for the charges enclosed by the surface, it shall not account for charges outside the surface.
Application of Gauss Law
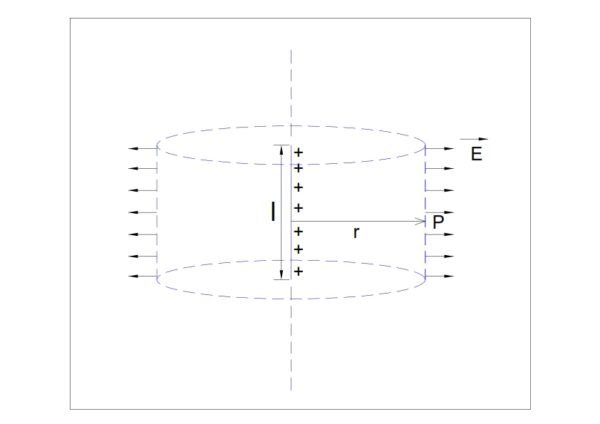
Gauss Law is very useful for calculating the Electric Field at any point. Let us use this law to find the value of field at any point P from a uniformly charged infinite long rod. Let the surface charge density of the infinitely long rod be λ.
Well, for applying Gauss Law very first step should be to draw a closed surface passing through point P. This closed surface is obviously a cylinder. Let the length of cylinder is ‘l’ and radius is ‘r’.
As the line is uniformly charged and its length is infinite, therefore the electric field on its curved surface will be uniform and perpendicular to surface. Thus the flux of electric field through the closed surface
Ø = ∫E.ds
Since the direction of area vector ds is perpendicular to the surface ds and outside the volume therefore area vector ds and E are parallel. Therefore their dot product E.ds = Eds. Hence,
Ø = ∫Eds
Since E is constant on the surface, therefore we can take it outside the integration.
= E ∫ds
But ds is the total curved surface area which is equal to 2πrl.
= Ex(2πrl)
But as per Gauss Law, the flux of net electric field is equal to the total charge enclosed divided by permittivity. Hence,
Ex(2πrl) = Qint / ξ0
Now, we need to find the total charged enclosed by the surface. Since surface charge density of line is λand the length of line enclosed by the closed surface is ‘l’ therefore Qint = λl.
Therefore,
Ex(2πrl) = λl / ξ0
⇒E = λ / 2πξ0r
The above expression gives the value of electric field at a distance r from the uniformly charged infinitely long rod.