j Operator and Its Significance

What is j Operator?

j Operator is a mathematical operator which when multiplied with any vector, rotates that vector by 90 degree in anti-clock wise direction. Just like symbols x, +, – etc. are used with numbers for indicating certain operations to be performed on those numbers, j operator is used to indicate the counter-clock wise rotation of a vector through 90°.

j operator has been assigned a value of √(-1). Thus, it is an imaginary number. The double operation of j on a vector rotates it in counter-clock wise direction through 180°.  Thus, the direction of vector gets reversed when double operation of j is performed on a vector. Therefore, we can write,

Explanation of j Operator:

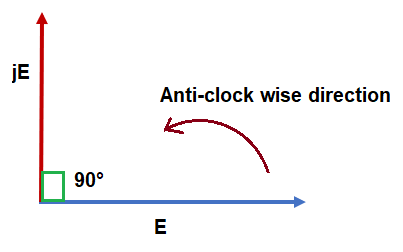
When operator j is operated on vector E, we get the new vector jE. This new vector jE is displaced from the original vector E by 90° in anti-clockwise direction. It may be noted that, the magnitude of vector remains unchanged when the vector is operated by j. This is shown in figure below.

If the “j” is applied on the vector jE, the new vector j₂E will be the 180° apart in anti-clockwise direction. This means, new vector j₂E is in opposite to the original vector E. Hence, we can say that, j²E = –E. For better understanding, you may refer the figure below.

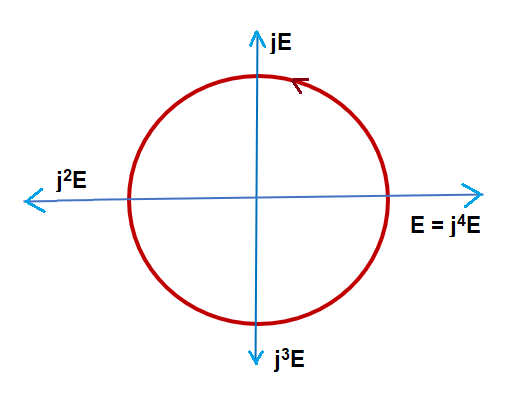
Similarly, when j²E is operated with j, the new vector so produced (j³E) will be 270° ahead of the E. Note that, this new vector is opposite to vector jE. Hence, we can say, j³E = jE. Similarly, j⁴E = E.

From the above discussion, we can list some of the important property of j operator. They are as follows:

• j² = -1
• j³ = (j²) x j = -j
• j⁴ = (j²)² = 1
• (1/j) = -j

Significance:

In Electrical Engineering, j operator has a great significance and application. You will encounter this operator often in electrical machine, power system, AC Network etc.

As we know that impedance of a circuit is a complex quantity i.e. it is having real part and imaginary part. Real part signifies resistive portion whereas imaginary part denotes reactance part of the impedance. As current through reactance either lags or lead the voltage by 90°, therefore, this reactance is represented by using j operator. The current through resistance remain in phase with the voltage, hence resistance is taken as reference and reactance (say X) is rotated with respect to this reference when operated with j operator. Hence, impedance Z is written as Z = (R ± jX). It may be noted that the capacitive and inductive reactance are (-j/ωC) and jωL.