What is Penalty Factor?
Penalty Factor in Power System is a factor (greater than unity) by which the incremental cost of power production of plant must be multiplied to accommodate for the transmission losses. It is also defined as the ratio of power generated by the plant to the actual power demand of the load being met after transmission loss. Let us understand this more clearly.
As we know that, for economic load dispatch, the incremental production cost of all operating plants should be equal. But this criterion is true only if the load and the power generating plants are localized. This means the power generated by the plant is supplies only the local loads. Suppose there is “n” number of power plants supplying the local loads (load center is nearby the generating station). To meet the power demand of PD, all these “n” plants should be so operated that their incremental power cost is same.
If F be the fuel cost in Rs. per hour for power P MW, then the incremental power cost will be (dF/dP). Note that, the unit of this incremental cost is Rs. per MWhr. If F1, F2, F3,…Fn be the fuel cost for power P1, P2, P3,….Pn, then as per equal incremental cost criteria,
(dF1/dP1) = (dF2/dP2)=…….=(dFn/dPn) = λ (say) ……(1)
for optimal operation of system for economic load dispatch. Here λ is incremental cost of power production in Rs. per MWhr.
Now, let us consider a system consisting of two identical generators with identical incremental production cost as shown in figure below.

If generator 2 has local load, the as per the equal incremental production criterion, both the generators should share the load equally (this is because the incremental production cost of both the generators 1 &2 are same). This means generator 1 should share half of the load whereas generator 2 should share remaining half of the load for economic operation. But as you can see, the load is concentrated near generator 2, therefore for economic operation; it will be wise to let the load fed by the generator 2 only. This is because; generator 1 will have to feed the transmission loss in addition to load. The more the load fed by the generator 1, the more will be associated transmission loss. This means, transmission loss is a function of power. Basically, it is directly proportional to square of power generated by the plant.
PL α (Power Generated)2
PL α Length of Transmission Line
Therefore, when load dispatch is associated with transmission loss, the concept of sharing load by equal incremental production cost does not hold good. Therefore (1) is not valid for such case. What should we don then to apply equal incremental production cost for load sharing to make economic load dispatch?
Hmmmmm……It is clear that for the above scenario, the incremental production cost of generator 1 will be higher. So what we can do that, we can multiply incremental production cost of generator 1 i.e. (dF1/dP1) by some factor (say K) more than unity so that it becomes equal to (dF2/dP2). So we can write,
(dF1/dP1)xK = (dF2/dP2) = λ
(dF1/dP1)xK = λ ……(2)
This multiplication factor K is called Penalty Factor for Generator 1. Why is it called Penalty Factor? This is because; generator 1 is being penalized due to additional transmission loss in its power production cost. Thus, penalty factor can also be defined as the ratio of cost incurred when transmission loss is taken into account to the cost incurred without having transmission loss. This definition gives better sense of penalty factor. Isn’t it?
Derivation of Penalty Factor:
Hope you understood the concept of penalty factor. Now we will derive its formula. To derive, first of all we will have a look at the Coordination Equation. Coordination equation is basically a mathematical equation which gives the relationship between incremental transmission loss with incremental cost of production. It is given as
(dFn/dPn) + λ(dPL/dPn) = λ
where PL is the transmission loss and (dPL/dPn) is known as the incremental transmission loss at plant “n”.
(dFn/dPn) = λ – λ(dPL/dPn)
= λ{1 – (dPL/dPn)}
(dFn/dPn) x[1/{1 – (dPL/dPn)}] = λ …….(3)
Comparing (2) and (3),
K = 1/{1 – (dPL/dPn)}
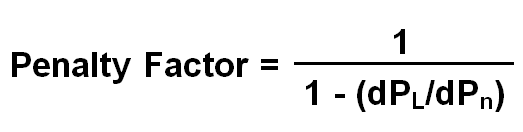
It should be noted that transmission loss PL is a function of power transmitted. The more the power transmitted, the more will be the loss. For tow generator system shown in the figure, the loss equation is given as
PL = B11P12 where B11 is called transmission loss coefficient.
Problems on Penalty Factor:
The problems or numerical on penalty factor are very important from examination point of view. Problem based on this concept is also asked in GATE exam. I will here demonstrate three numerical on penalty factor which will clear your concept.
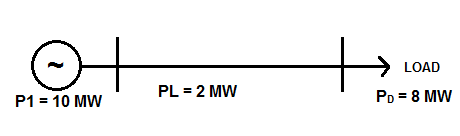
Example-1: Determine the penalty factor of plant shown in figure below. Also find the cost of power if incremental cost of power production is
dF1/dP1 = 0.1P1 + 3.0 Rs/MWhr
Solution:
The power generated by plant = 10 MW
Transmission Loss = 2 MW
Power Delivered to Load = 8 MW
As penalty factor is the ratio of power generated to power fed to the load, therefore
Penalty Factor = 10/8 = 1.25
Cost of Power Generated
= Incremental Cost x Penalty Factor
But incremental cost of power of 10 MW
= 0.1×10 + 3
= 4 Rs/MWhr
Cost of Power Generated
= 4×1.25
= 5 Rs./MWhr (Ans.)
Example-2: (This question has been asked in GATE-2012)
Figure below shows a two generator system supplying a load PD = 40 MW, connected at Bus-2.
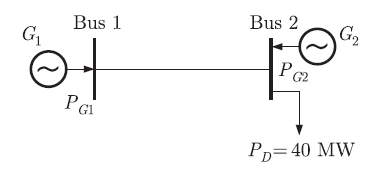
The fuel cost of generator G1 and G2 are
C1(PG1) = 10000 Rs/MWhr and C2(PG2) = 12500 Rs/MWhr and the loss in the line is Ploss(pu) = 0.5(PG1)2, where the loss coefficient has been expressed in pu on a base of 100 MVA. Find the most economic power generation schedule of the plants.
Solution:
In the above system of two generators and load, the load is local to the generator G2. Therefore Generator 2 won’t have any penalty factor. But Generator 1 will have to feed transmission line losses in addition to load, therefore it will have a penalty factor. Let us first find the penalty factor of G1.
Since, PL = Transmission Loss = 0.5(PG1)2
(dPL/dPG1) = 0.5x2PG1 = PG1
Penalty Factor = ……(4)
Therefore to get most economic power generation schedule,
(dFG1 / dPG1) x Penalty Factor = (dFG2 / dPG2)
Where (dFG1 / dPG1) and (dFG2 / dPG2) are incremental fuel cost in Rs. / MWhr of generator 1 and 2 respectively. But,
(dFG1 / dPG1) = 10000 Rs/MWhr
(dFG2 / dPG2) = 12500 Rs/MWhr
Therefore,
10000x[1 / (1- PG1)] = 12500
⇒1 / (1- PG1) = 12500 / 10000
⇒(1- PG1) = 10000 / 12500
⇒PG1 = 2500 / 12500
= 0.2 pu
Assuming base of 100 MVA,
PG1 = 0.2×100 = 20 MW (Ans.)
Loss in Transmission line PL = 0.5x(0.2)2
= 0.02 pu
Assuming base of 100 MVA, transmission loss = 0.02×100 = 2 MW
Thus the actual load fed by the Generator 1 = (20-2) = 18 MW
Since total load is 40 MW, remaining load will be fed by generator 2. Thus,
PG2 = (40-18) MW = 22 MW (Ans.)
Example-3: (This question has been asked in GATE-2011)
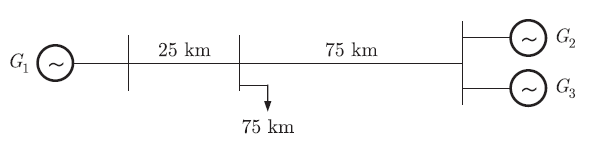
A load center of 120 MW derives power from two power stations connected by 220 kV transmission line of length 25 km and 75 km as shown in figure below. The three generators G1, G2 and G3 each of capacity 100 MW have identical fuel cost characteristics.
The minimum loss generation schedule for supplying 120 MW load is
- P1 = 80 MW + Losses , P2 = 20 MW, P3 = 20 MW
- P1 = 60 MW, P2 = 30 MW + Losses, P3 = 30 MW
- P1 = 40 MW, P2 = 40 MW, P3 = 40 MW + Losses
- P1 = 30 MW + Losses , P2 = 45 MW, P3 = 45 MW
Which of the above option is correct?
Solution:
As can be seen from the figure that,
- G2 & G3 are located at the same distance from the load and have same fuel characteristics. This means they will share load equally.
- Since the distance of load from G2 & G3 is 75 km so both these generators should share lower value of load to avoid higher transmission loss.
- Distance of load from G1 is 25 km (which is less than 75 km), therefore this generator should share most of the load as the transmission loss will be lower.
With the above three points, it is clear that option 1) is correct. (Ans.)