Principle of Induction Type Relays

All the relays operate in response to one or more electrical quantities either to close or to open contacts. There are really only two fundamentally different operating principles:

• Electromagnetic Attraction, and

• Electromagnetic Induction.

Electromagnetic attraction relays operate by virtue of a plunger being drawn into a solenoid, or an armature being attracted to the poles of an electromagnet. Such relays may be actuated by DC or by AC quantities. Visit Induction Relay – Construction Detail to know about constructional feature of Induction Relay.

Electromagnetic-induction relays use the principle of the induction motor where torque is developed by induction in a rotor; this operating principle applies only to relays actuated by Alternating Current, and called Induction Type relays.

Induction-type relays are the most widely used for protective-relaying purposes involving AC quantities. They are not usable with DC quantities, because of their principle of operation.

An Induction Type Relay is a split-phase induction motor with contacts. Actuating force is developed in a movable element that may be a disc or other form of rotor of non-magnetic current-conducting material by the interaction of electromagnetic fluxes with eddy currents that are induced in the rotor by these fluxes.

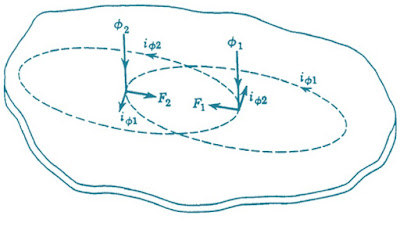
Figure below shows how force is produced in a section of a rotor that faces two adjacent AC fluxes. Various quantities are shown at an instant when both fluxes are directed downward and are increasing in magnitude. Each flux induces voltage around itself in the rotor, and currents flow in the rotor under the influence of the two voltages. The current produced by one flux reacts with the other flux, and vice versa, to produce forces that act on the rotor.

The quantities involved in an Induction Type relay may be expressed as follows:

Ø₁ = Ø_1msinwt

Ø₂ = Ø_2msin (wt + Ɵ)

Where Ɵ is the phase angle by which Ø₂ leads Ø₁. It may be assumed with negligible error that the paths in which the rotor currents flow have negligible self-inductance, and hence rotor currents are in phase with their voltages:

iØ₁ ∝ d Ø₁ / dt ∝ Ø₁coswt

iØ₂ ∝ d Ø₂ / dt ∝ Ø₂cos (wt+Ɵ)

As clear from the figure shown above, the two forces F1 and F2 are in opposition, and consequently we may write the equation for the net force (F) as follows:

F = (F₂ – F₁)

    ∝ (Ø₂i_Ø1– Ø₁i_Ø2)  …………………..(1)

Putting the values of the quantities into equation (1), we get

F ∝ Ø_1mØ_2m[sin (wt + Ɵ)coswt – cos (wt + Ɵ)sinwt ]  ………….(2)

Therefore,

F ∝ Ø1mØ2mSinƟ

Thus the actuating force in an Induction Type Relay is directly proportional to the phase displacement between the two fluxes. For maximum actuating force, the phase displacement Ɵ must be 90°.

Thus to summarize, actuating force is produced in the presence of out-of-phase fluxes. One flux alone would produce no net force. There must be at least two out-of-phase fluxes to produce any net force, and the maximum force is produced when the two fluxes are 90° out of phase. Also, the direction of the force-and hence the direction of motion of the relay’s movable member-depends on which flux is leading the other.

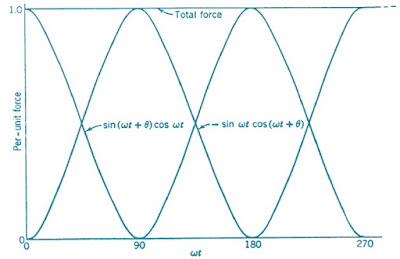
A better insight into the production of actuating force in the induction relay can be obtained by plotting the two components of the expression inside the brackets of equation (2). Figure below shows such a plot when Ɵ is assumed to be 90°. It shall be observed that each expression is a double-frequency sinusoidal wave.

The two waves are displaced from one another by 90° in terms of fundamental frequency, or by 180° in terms of double frequency. The sum of the instantaneous values of the two waves is 1.0 at every instant. If Ɵ were assumed to be less than 90°, the effect on Figure above would be to raise the zero-force axis, and a smaller per-unit net force would result. When Ɵ is zero, the two waves are symmetrical about the zero-force axis, and no net force is produced. If we let Ɵ be negative, which is to say that Ø₂ is lagging Ø₁, the zero-force axis is raised still higher and net force in the opposite direction is produced. However, for a given value of Ɵ, the net force is the same at each instant.