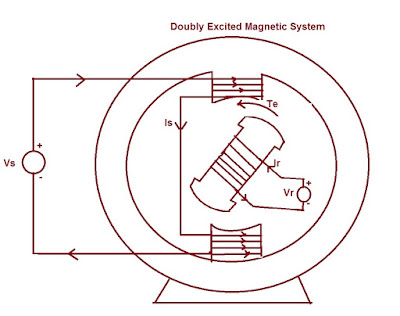
Lets us consider a doubly excited magnetic system as shown in figure below. In this model of machine, both stator as well as rotor is assumed to be salient pole type. Let’s assume that stator is energized from source Vs whereas rotor is energized with source Vr.
Total torque developed in such doubly excited magnetic system is given as
Te = (Is2/2)(dLs/dƟr) + (Ir2/2)(dLr/dƟr) + IsIr(dMsr/dƟr)
Case1: If rotor current is made zero i.e. Ir = 0
Torque Te = (Is2/2)(dLs/dƟr)
Thus we see that even though rotor current is zero, an electromagnetic torque is developed as the Reluctance seen by the stator produced flux changes with the position of rotor Ɵr. A change of reluctance seen by stator produced flux varies the self inductance of stator winding Ls with Ɵr.
Case2: If stator current is made zero i.e. Is = 0
Torque Te = (Ir2/2)(dLs/dƟr)
Thus we see that even though stator current is zero, an electromagnetic torque is developed as the Reluctance seen by the rotor produced flux changes with the position of rotor Ɵr.
In view of the above two cases, we can say that the torque expressions as obtained in two cases are Reluctance Torque as this torque is not produced by the interaction of two fluxes rather this torque is produced just because of change of reluctance and hence a change in self-inductance.
To have a physical understanding of the Reluctance Torque let s consider the doubly excited magnetic system as shown in figure above. If only stator of the system is excited, then the stator flux would have a tendency to follow less reluctance path for which the rotor turns anticlockwise direction. Now if only rotor is excited, rotor produced flux would have a tendency to follow minimum reluctance path and for achieving this rotor will again turn anticlockwise.
In the figure shown above in the discussion, suppose the salient rotor is replaced with cylindrical rotor and is excited by current Ir. As the rotor is cylindrical, the reluctance en by the stator produced flux will be same irrespective of the rotor position Ɵr. Thus the self-inductance of stator winding Ls will be a constant quantity and hence dLs/dƟr = 0 which in turn means that no reluctance torque will be present. Therefore the equation of torque becomes,
Te = (Ir2/2)(dLr/dƟr) + IsIr(dMsr/dƟr)
Note that as the stator poles are salient in the figure, the reluctance seen by the rotor produced flux will vary with the position Ɵr and hence there will a change in self-inductance of rotor Lr, this why reluctance torque term (Ir2/2)(dLr/dƟr) is appearing in the above torque equation.
To summarize, we can say that the first two terms in the generalized torque equation of doubly excited magnetic system, are Reluctance Torque.
Te = (Is2/2)(dLs/dƟr) + (Ir2/2)(dLr/dƟr) + IsIr(dMsr/dƟr)
It shall also be noted from the reluctance torque term that Reluctance Torque, is independent of direction of current in stator and rotor windings.
Last term i.e. IsIr(dMsr/dƟr) represents that component of total torque which depend on both rotor and stator current and also on the angular rate of change of mutual inductance Msr. This component of Torque is called Electromagnetic Torque. From the electromagnetic torque term IsIr(dMsr/dƟr), following conclusion can be drawn:
“Electromagnetic torque can only exist if the two winding i.e. stator and rotor are mutually coupled and both winding carry current.”
The physical concept of electromagnetic torque in figure shown previously in the discussion is as follows:
The North, South poles produced on stator by current Is and South and North poles produced on rotor by current Ir attract each other tending to align their fields. The torque so developed by the interaction of stator and rotor magnetic field is the electromagnetic or interaction torque. Electromagnetic torque or interaction torque depends on the direction of current in stator and rotor windings.
In the figure, the direction of electromagnetic torque for current stator and rotor current is anticlockwise. If the direction of rotor current Ir is reversed, the interaction or electromagnetic torque will be reversed i.e. in clockwise direction but the direction of Reluctance Torque would still remain in the same direction as before i.e. anticlockwise.
SIR FOLLOWING IS A QUESTION IN "JB GUPTA ELECTRICAL QUESTION BANK"
A rotating electrical machine having its self inductance of both stator and rotor winding independent of its rotor position will definitely not develop:
1. SYNCHRONISING TORQUE
2. RELUCTANCE TORQUE
3. STARTING TORQUE
4. HYSTERESIS TORQUE
and the answer given is synchronising torque but after reading your blog i think answer should be RELUCTANCE TORQUE as dL/d0 will be zero so no reluctance will be present.
Please explain Sir.
Since self inductance of rotor as well as stator is independent of rotor position, there will not be any reluctance torque for your question. Electromagnetic torque will be present like in synchronous generator.
Thank You
PLEASE EXPLAIN THIS QUESTION:
An electric train driven by a dc series motor is running at a fixed speed when a sudden reduction in mains voltage occurs. This would result in::
Drop in Speed and Rise in Current…..How??
You are requested to post questions of other topic in "Ask Question" section. Thank you!