Single Line to Ground Fault Analysis

In earlier posts we discussed, Concept of Symmetrical Components and Calculation of Symmetrical Components. It is recommended to go through these topics before analyzing Single Line to Ground Fault.

Because of ground fault in A phase, the voltage at the point of fault will become zero and current through the other phases i.e. B and C phases will become zero. Therefore we can write as

V_a = 0

I_b = 0

I_c = 0

Therefore, from the Calculation of Symmetrical Components, we can write as

I_a0 = (I_a + I_b + I_c)/3

      = I_a/3

I_a1 = (I_a + λI_b + λ²I_c)/3

      = I_a/3

and,

I_a2 = (I_a + λ²I_b + λI_c)/3

      = I_a/3

From the above expressions of positive, negative and zero sequence components of current in faulted phase A, we observe that all the sequence currents are equal in magnitude and phase. Thus for faulted phase, in case of Single Line to Ground Fault, we can write

I_a0= I_a1 = I_a2 = I_a/3

Calculation of Fault Current:

First thing which must be understood at this point, that fault current is completing its path through the grounded neutral. If there were no any grounded neutral, no fault current would have been flow.

We will apply Kirchhof’s voltage law here to find the fault current. As fault current is only flowing in the faulted phase A, therefore we are only interested in finding Ia.

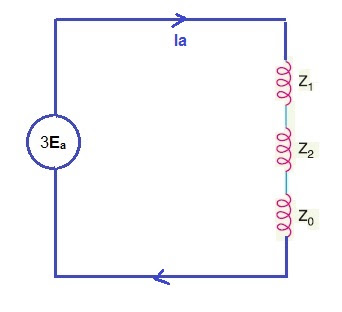
E_a = V_a + I_a0Z₀ + I_a1Z₁+ I_a2Z₂

     = 0 + I_a0Z₀+ I_a1Z₁ + I_a2Z₂

⇒ E_a = I_a0Z₀ + I_a1Z₁ + I_a2Z₂

But I_a0 = I_a1= I_a2 = I_a/3 so,

E_a = I_a/3 Z₀ + I_a/3 Z₁ + I_a/3 Z₂

⇒ I_a = 3E_a / (Z₀ + Z₁+ Z₂)

From the above expression of fault current, it is quite clear that positive, negative and zero sequence impedance are connected in series for Single Line to Ground Fault and the equivalent circuit may be represented as shown below.

The above expression for fault current has been derived assuming that the neutral of the system is solidly grounded. For a system where neutral is grounded through some finite resistance, say Z, then the fault current would be given as

I_a= 3E_a / (Z₀ + Z₁ + Z₂+ Z)

It shall also be noted that, for ungrounded system or isolated neutral system as there is no path for neutral current to flow, therefore the impedance seen by zero sequence current will be infinite (as only zero sequence current flows through the neutral) and hence the value of zero sequence component of fault current will be zero.

You may like to read Concept of Neutral Grounding.

Calculation of Voltage of Healthy and Faulty Phases:

Since the generated voltage of Generator is positive sequence voltage, therefore

E_a0 = 0

E_a1 = Ea

E_a2 = 0

Now, the positive sequence voltage at the point of fault

V_a1 = E_a – I_a1Z₁

      = E_a – E_aZ₁/ (Z₀ + Z₁+ Z₂)

⇒ V_a1 = (Z₂ + Z₀)E_a/ (Z₀ + Z₁ + Z₂)

Similarly,

V_a2= 0 – I_a2Z₂

        = –E_a Z₂/ (Z₀ + Z₁ + Z₂)

and

V_a0  = 0 – I_a0Z₁

       = E_a Z₀/ (Z₀+ Z₁ + Z₂)

Thus we have calculated the sequence components of voltages of faulty phase. For calculating the voltages of healthy phase we will apply the concept of symmetrical components as shown below.

V_b= V_b0 + λ²V_b1 + λV_b1

V_c= V_c0 + λV_c1 + λ²V_c1

In this way, we can calculate the level of earth fault current in Single Line to Ground fault and voltages of different phases.