Superposition theorem states that the resultant current in any branch in a liner network having a number of sources, is the algebraic sum of the current that would be produced in it, when each source acts alone replacing all other independent sources by their internal resistance. This theorem is very useful for solving a network having two or more source which are neither connected in series no parallel. Therefore, a thorough understanding of superposition theorem is very important to deal with circuit theory. In this article, we will discuss Superposition Theorem, application, formula and steps to solve problem.
Superposition Theorem Statement may be interpreted as, if there are a various source whether current or voltage source in a linear circuit, the current in any branch of circuit may be calculated by assuming one source at a time and replacing all other sources by their internal resistance. This essentially means that, an ideal voltage source should be shorted while a current source should be kept open circuit while solving problem related to Superposition Theorem. While calculating the current through any particular branch, direction of current due to individual source must be taken care to get the total or resultant current.
Explanation of Superposition Theorem:
To better understand superposition theorem, let us consider a circuit shown below.
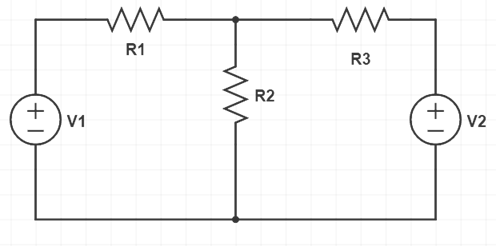
In this circuit, there are two sources V1 and V2. Both these sources are neither connected in parallel nor in series. Suppose, we want to find the current through resistance R2 using superposition theorem.
To apply the theorem, first of all, we replace any one source by its internal resistance. Let us replace V2 first. Since V2 is an ideal source, hence it will be replaced by a short in between its terminal. This is shown in figure below.

The current through resistance R2 is assumed to I2 and may be calculated as shown below.

As a next step, we will deactivate source V1 and replace it by a short. Then we will again calculate current through resistance R2. Figure below shows this step.

Let us now find the current through resistance R2 due to source V2 alone. This current can be calculated in the similar fashion as calculated above.

Thus, we have calculated the current through resistance R2 due to both the sources when they are acting alone. Now, as per superposition theorem, the resultant current through R2 will be the sum of I2 and I2’. This is because, the direction of current for both the sources are same and hence they are added up to get the total current. If the currents would have been in opposite direction, then they must have been subtracted to get the total current.
Resultant Current through R2
= I2 + I2’
Steps for Solving Network using Superposition Theorem:
The steps for solving circuit using superposition theorem is quite easy. They are as follows:
Step-1: Take only one independent source of voltage / current and deactivate all other independent sources. For voltage source, remove the source and short circuit the respective circuit terminals and for current sources, just delete the source while keeping its terminals open.
Calculate the current in the required branch of circuit when only one source is present.
Step-2: Repeat the above step for each of the independent sources.
Step-3: To determine the net branch current, add the currents obtained in above two steps. If the current obtained in Step-1 & Step-2 are in the same direction, simply add them. If the respective currents are directed opposite, then currents should be subtracted.