Maximum Power Transfer Theorem states that, for any type of circuit whether ac or dc, maximum amount of power is delivered from source to load when the source impedance as viewed from the load terminal is equal to the load impedance. This theorem is used to find the value of load impedance for which there would be a maximum amount of power flow from source to load. In this article, maximum power transfer theorem, derivation, efficiency and steps for its application is explained with the help of solved problems.
Explanation of Maximum Power Transfer Theorem:
In dc circuit, the impedance of circuit is equal to the resistance. Therefore, maximum power transfer theorem may be stated as, to deliver the maximum power from source to load, the load resistance must be equal to the source resistance or Thevenin resistance. Here, Thevenin resistance essentially means the resistance of source network when viewed from the load terminals.
Let us consider a dc circuit as shown below for better understanding of Maximum Power Transfer Theorem.
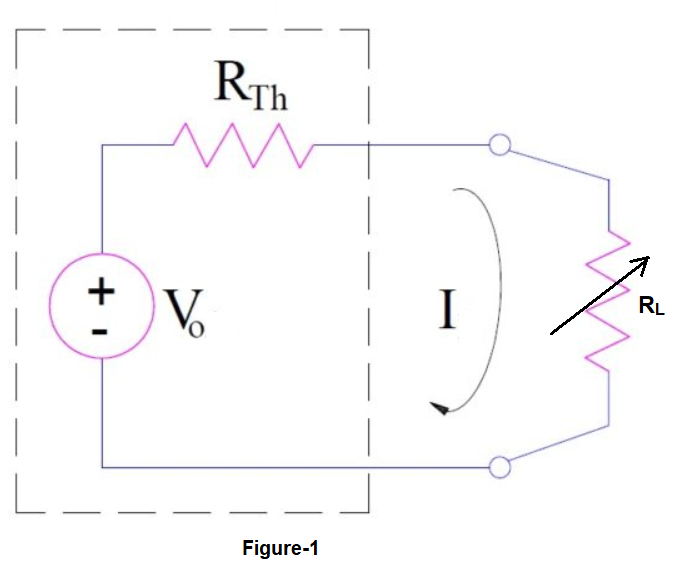
A variable load resistance RL is connected to the dc source network. The value of Thevenin voltage is Vo while the source network resistance when viewed from load terminal (this is called Thevenin resistance) is RTh. Therefore, according to maximum power transfer theorem, the formula for maximum power flow from source to load will is given as below.
Load Resistance, RL = Thevenin Resistance, RTh
Maximum Power Transfer Theorem Derivation:
For maximum power transfer theorem derivation, first of all we will calculate the current flowing through the circuit. Then, power (P) dissipated in the load resistance is equal to the I2RL i.e. P = I2RL. Now, we will differentiate this power P with respect to RL (as RL is a variable quantity) and equate it to zero. This will give us the value of RL for which maximum power will flow from source to load. This concept may be followed to get the proof of the theorem
Let us now apply the above concept and derive the maximum power transfer theorem. Refer the dc circuit shown in figure-1. Let us first calculate the current through the load resistance RL. The current I through the circuit is given as below.

Now, power dissipated in load resistance RL due to this current I is the power delivered from source to load. Therefore, it will be a wise decision to find the power dissipated in RL due to I. Let this power be P.
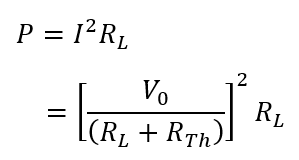
As power P is a function of RL, therefore, to get maximum value of “P” we differentiate P w.r.t RL and equate it to zero. This is shown below.
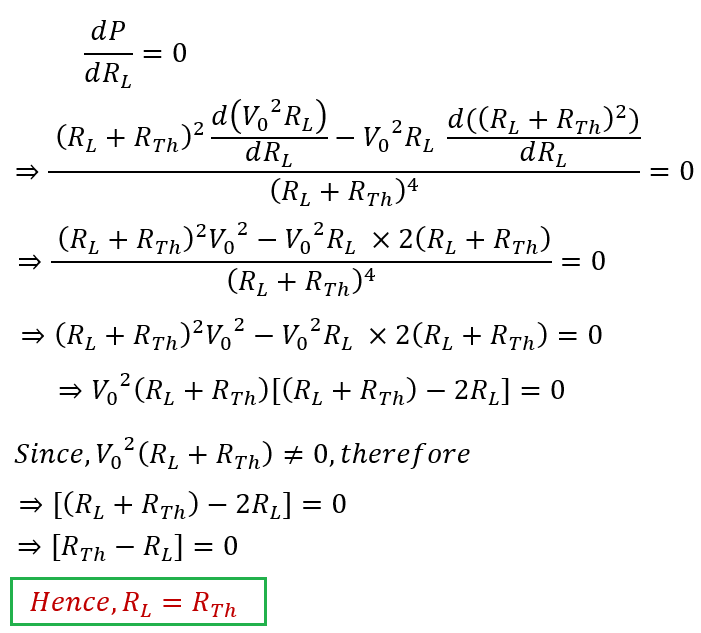
Therefore, it is proved that, the value of load resistance and source resistance should match for maximum power delivery to the load from a dc source network. Let us now calculate the efficiency during the condition of maximum power transfer.
Maximum Power Delivered to Load:
Under the condition of maximum power delivery, the current through the circuit is given as below.
I = (Vo/2RTh)
Therefore, maximum amount of power transferred to load
= I2RL
= I2RTh (RL = RTh)
= [(Vo)2/4RTh]
Efficiency:
Efficiency during maximum power transfer is the ratio of power dissipated in load to the total power supplied by the source. The value of this efficiency is 50%.
During maximum power transfer, source resistance and load resistance are equal as derived. This means, RL = RTh. Also, the current “I” is flowing through RTh as well as RL. Therefore, the power dissipated in load will be equal to the power dissipated in source internal resistance RTh. Hence, the total power delivered by source will be equal to the sum of power dissipated in load as well as internal resistance.
Total Power Delivered by Source Ps
= Power dissipated in RL + Power dissipated in load RTh
= I2RL + I2RTh
= I2 (RL+ RTh)
= 2 I2 RL (since, RL = RTh)
= 2 PL (PL is power dissipated in load)
Therefore,
Efficiency = PL / Ps
= PL / 2PL
= 0.5
Hence, percentage efficiency during maximum power transfer condition
= 0.5×100
= 50%
Application of Maximum Power Transfer Theorem (MPTT):
The concept of maximum power transfer theorem finds a wide application in communication circuits. In communication circuit, the magnitude of power transfer is very small and hence low efficiency of 50% is not a problem for such applications. However, in electrical power transmission system, the efficiency of 50% is not tolerable at all. This simply means that, half of the total generated power is lost before reaching the load center. The main aim of power transmission is to maintain voltage or minimize the voltage drop and line losses. In view of this, MPTT is not applicable for power transmission.
Steps to Solve Maximum Power Transfer Theorem:
The steps to solve maximum Power Transfer Theorem is quite simple and handy. Following are the sequential steps:
Step-1: Remove the load resistance (RL) and find the Thevenin resistance (RTh) of the source network when viewed from the open circuited terminals of load.
Step-2: For maximum power delivery from source to load, this Thevenin resistance should be equal to load resistance. This essentially means, RL = RTh
Step-3: Find the Thevenin voltage (Vo) across the open circuited terminals of load. If you find problem in calculating this value, kindly refer Thevenin Theorem.
Step-4: Maximum amount of power delivered to load is equal to [(Vo)2/4RTh]
Maximum Power Transfer Theorem Solved Problem:
In this section, we will solve one problem related to the theorem. This will definitely help you to better understand and summarize the concept of maximum power transfer theorem.
Problem: Find the value of maximum power dissipated in RL in the circuit shown below. Provided r = 5 Ω, v0 = 10 V and i0 = 2 A.

Solution: To solve this problem, we will follow the steps discussed earlier in this article. As the very first step, we will remove the load resistance RL and find the Thevenin resistance.
Step-1: Remove RL and find Thevenin resistance. To find the Thevenin resistance, we will short the voltage source and current source will be replaced by open circuit.
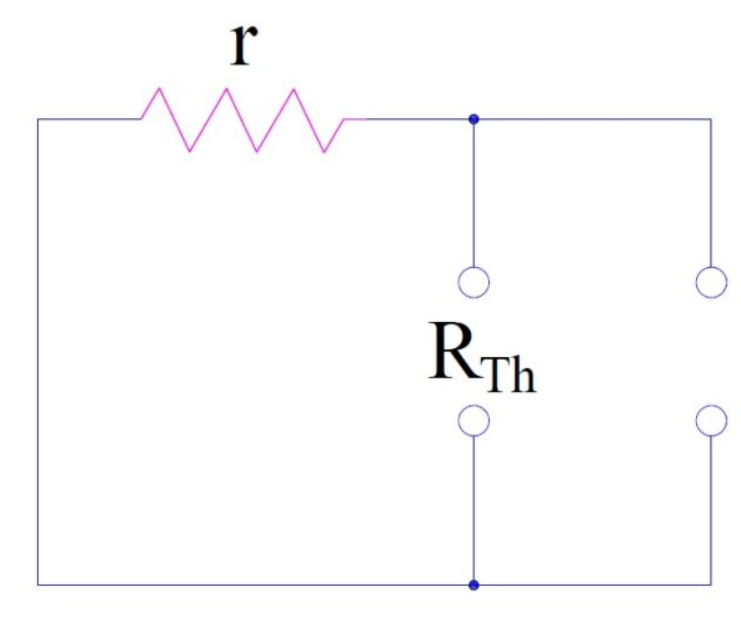
Thus, the Thevenin resistance Rth = r = 5 Ω.
Step-2: For maximum delivery of power to the load resistance, the value of load resistance RL should be equal to Thevenin resistance i.e. 5 Ω.
Step-3: In this step, we will find the voltage across the open circuited load terminals. This is called Thevenin voltage.
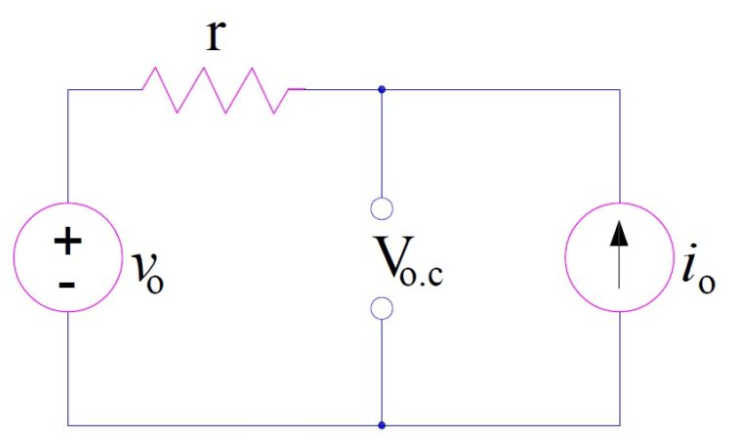
Voc = ri0 + v0
= (5×2 + 10) V = 20 V
Step-4:
Maximum power transferred to load
= (20)2/(4×5)
= 20 Watt (Ans.)