Voltage Regulation of a Transformer

Voltage Regulation of Transformer is defined as change in magnitude of Secondary Terminal Voltage per unit Rated Secondary Terminal Voltage when load at a given Power Factor is reduced to zero while maintain the Primary Voltage constant.

Transformer Voltage Regulation = (E₂– V₂) / E₂ in pu

                                = (E₂– V₂) x100 / E₂ in percentage.

The change in magnitude of Secondary Terminal Voltage with loading of Transformer is because of Primary and Secondary leakage impedance. The magnitude of this change in voltage depends on the load current, load power factor, total leakage reactance and total resistance of Transformer.

As the consumer need their terminal voltage to be within a prescribed limit, the Voltage Regulation of a Distribution Transformer shall be less i.e. good. For better Voltage Regulation of a Distribution Transformer, it is quite important that their leakage impedance shall be less.

Calculation of Transformer Voltage Regulation:

The Voltage Regulation of a Transformer can be obtained from its equivalent circuit model when referred to Primary or Secondary side. Figure below shows the equivalent circuit of a Transformer when referred to Secondary side and its phasor diagram for load of lagging power factor.

In the figure above,

re2 = Equivalent resistance referred to Secondary

xe2 = Equivalent reactance referred to Secondary

It can be seen from the above phasor diagram that,

E₂ ≈ OC

      = OA + AB + BC

But from the right angled Triangle ABE,

CosƟ₂ = AB / AE

So, AE = ABCosƟ₂

            = I₂r_e2CosƟ₂

Similarly from the right angled Triangle DEF,

Therefore BC = EF = I₂x_e2SinƟ₂

E₂ = V₂+ I₂r_e2CosƟ₂ +I₂x_e2SinƟ₂

Hence,

(E₂ – V₂) = I₂r_e2CosƟ₂ +I₂x_e2SinƟ₂ 

Now, per unit Voltage Regulation for any load current I₂,

(E₂ – V₂) / E₂ = I₂r_e2CosƟ₂ / E₂+I₂x_e2SinƟ₂ / E₂

 In case I2 is rated current then,

  I₂r_e2 / E₂ = Voltage drop across re2 at rated current / Rated Voltage

                   = pu resistance drop

                   = ε_r     ………………..(1)

Similarly,

I₂x_e2/ E₂ = Voltage drop across reactance / Rated or Base Voltage  

                 = pu reactance drop

                 = ε_x   ………………………(2)

Therefore pu Voltage Regulation VR at rated current,

VR = ε_rCosƟ₂ + ε_xSinƟ₂    

And percentage Voltage Regulation VR at rated current,

VR = (ε_rCosƟ₂ + ε_xSinƟ₂) x 100 %

The above calculation for Voltage Regulation has been carried out assuming lagging power factor load but for leading power factor load we only need to replace Ɵ2 by – Ɵ2. Therefore Voltage Regulation VR for leading power factor load for rated current will be as below.

VR = ε_rCosƟ₂ – ε_xSinƟ₂in pu.

       = (ε_rCosƟ₂ – ε_xSinƟ₂) x 100 %

Now we will investigate some conditions based on Voltage Regulation which are very important.

Condition for Zero Voltage Regulation of Transformer:

As can be seen from the expression of Voltage Regulation, that VR varies as the Power factor of load is varied keeping load current constant. Thus for a particular Power Factor, we can get zero Voltage Regulation.

As VR = 0

ε_rCosƟ₂+ ε_xSinƟ₂ = 0

So,

tanƟ₂ = – ε_r/ ε_x

From equation (1) and (2),

tanƟ2  = -r_e2 / x_e2 

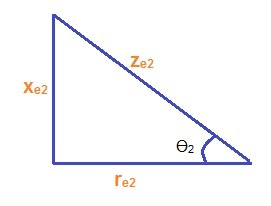
Therefore Magnitude of Power Factor CosƟ₂ = x_e2 / z_e2

Here negative sign in the value of tanƟ₂ means that power factor of load is leading. Thus zero Voltage Regulation is achieved by leading load of power factor x_e2 / z_e2 and if we increase the power factor of load beyond this value then Voltage Regulation will become negative. Negative Voltage Regulation means that Secondary Terminal Voltage V₂ is more than the no load generated EMF E₂.

Condition for Maximum Voltage Regulation of Transformer:

For Maximum Voltage Regulation,

d(VR) / dƟ₂ = 0 assuming load current constant.

Thus,

-ε_rSinƟ₂+ ε_xCosƟ₂ = 0

This implies that, tanƟ₂= ε_x / ε_r

Thus, CosƟ₂ = r_e2/ x_e2

Here tanƟ₂ is positive, which means that maximum Voltage Regulation occurs for lagging power factor load and at a power factor of r_e2 / x_e2.

One important thing to note here that,

Leakage Impedance Angle = Ø

                                            = Ɵ₂

Thus we can say that, maximum Voltage Regulation occurs when load power factor is equal to leakage impedance angle.