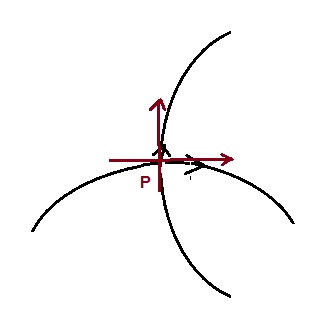Definition:
A point charge at rest creates a force field in its surrounding. This force filed is known as Electric Field. You can understand force field like a field created by a magnet in its surrounding due to which iron piece get attracted toward the magnet. Another example of force field is gravitational field. Thus, it is a force field created by a static charge. It is a vector quantity. Thus, it must have magnitude as well as direction.
Electric Field Intensity:
Electric Field Intensity at a particular point in space is defined as the force on a unit test charge. Basically, it is a parameter to measure the strength of electric field. It is denoted as E. Note here that, +1 C of charge is known as unit test charge.
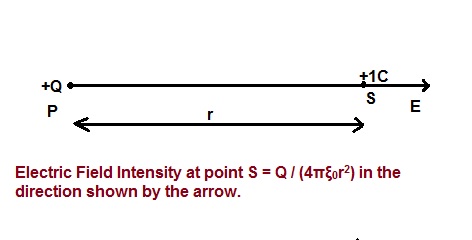
Let us assume that, a point charge of magnitude +Q is lying at some point P as shown in figure below. Now, we want to find the magnitude as well as the direction of Electric Field Intensity at point S.
Therefore, we will keep a unit test charge at point S and will find the magnitude and direction of force on this unit test charge. Well, to find the magnitude and direction of force on unit test charge, we will use Columb’s Law.
Therefore,
Magnitude of Electric Field E at point S = Columb’s Force on Test Charge at S
= Q / (4πξ0r2)
Hence, Magnitude of Electric Field Intensity at point S = Q / (4πξ0r2)
As two similar charges repel each other, therefore +Q charge will exert a force on the test charge as shown by the arrow in the figure above. This is the direction of Electric Field Intensity at point S.
Thus Electric Field Intensity due to a point charge +Q at some distance r is Q / (4πξ0r2) in a direction determined by Columb’s Law.
Calculation of Electric Field:
Whenever you need to find the electric field intensity vector at any point, follow these steps:
- Keep a unit test charge i.e. +1 C at the point
- Find the resultant force on the unit test charge by the point charges. Mind here that, if there are more than one charge then you need to find the resultant of individual forces.
- The magnitude of resultant force is the Electric Field Intensity at that point and the direction of resultant force gives the direction of Electric Field Intensity at that point.
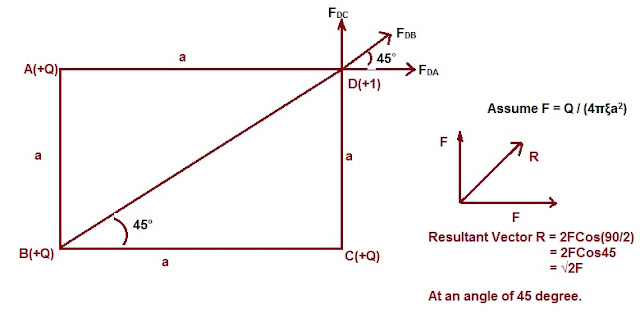
Example: Four charges of equal magnitude +Q are kept at the three corners of a square of side ‘a’. Find the electric field intensity vector at fourth corner.
Let’s first draw the figure as shown below.
Step 1: Keep a unit test charge at point D.
Step2: Find the resultant force on unit test charge.
Force on test charge at D due to charge at A, FDA = Q / (4πξa2)
Force on test charge at D due to charge at C, FDC = Q / (4πξa2)
Force on test charge at D due to charge at B, FDB = Q / (4πξ(√2a)2)
= Q / (8πξa2)
[As the distance between charge at C and test charge at D = Diagonal of Square = √2a]
Now, we need to find the resultant of FDA, FDB and FDC. Bold sign indicates vector form.
Since FDA = FDC = Q / (4πξa2) = F (say)
We know that, resultant of two equal vectors at an angle Ɵ is 2FCos(Ɵ/2). The direction of this resultant vector is at an angle of Ɵ/2 from either of the vector. Hence, here the resultant of FDA and FDC i.e. R will be
FDA + FDC = R = 2FCos(90/2) at an angle of 45°.
= √2F at an angle of 45°.
Now, resultant vector R and FDB are along the same along the same line making an angle of 45 degree from origin.
Therefore,
Net force on unit test charge at point D = R + FDB
= √2F + Q / [4πξ(√2a)2]
= √2Q / (4πξa2) + Q / (8πξa2)
= {Q / (4πξa2)} [√2 + 1/2]
= [√2 + 1/2]Q / (4πξa2)
Thus the electric field intensity vector at point D has a magnitude of [√2 + 1/2]Q / (4πξa2) and direction as shown in figure above. Hope you understand the thing.
Electric Field Lines and their Significance
We now know how to find the direction of electric field intensity vector at a particular point. Electric Field lines are nothing but the graphical representation of electric field due to a charge in the space. It is also know as electric lines of forces.To draw electric field lines, we find the direction of electric field intensity vector at different points around the charge and make a plot.
Electric Lines of Forces due to a Point Charge
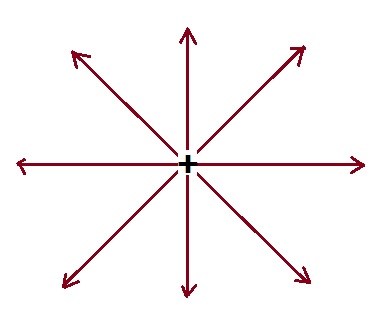
Electric Field due to a single point positive charge can easily be calculated at different points in the space using Columb’s Law and the method explained. If you find the direction of electric field intensity at different points and plot it, you will notice that it is radially outward and emanating from the charge. This is very clear as positive charge will repel the test charge.
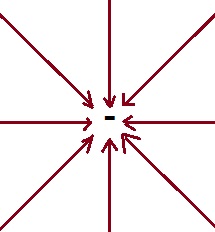
Similarly, the electric field due to a negative point charge is radially inward and terminates at negative charge. This is shown in figure. It is also quite obvious as negative charge attracts test charge.
Suppose two charges +Q and –Q are separated by some distance and we need to draw the field lines. In this case, we will follow the same method but this time, we will find the resultant direction of field at a particular point due to both charges. If you draw, the field lines will look like as shown below in the figure.
Properties of Electric Filed Lines
- The tangent at a particular point to the electric lines of force gives the direction of electric field intensity vector at that point.
- If the electric lines of force originate isotropically then electric field is proportional to the number of lines passing through unit area. Didn’t understand? Let’s consider an example. Consider two points P1 and P2 as shown in figure above. Draw equal small areas through P1 and P2 perpendicular to the lines. More number of lines passes through the area at P1 and less number of lines pass through the area at P2. Thus the strength of electric field at P1 will be more than that at P2.
- Two electric field lines can never intersect.
Why electric field lines can never intersect?
Let’s assume, the two field lines are intersecting at point P as shown in figure below.
We draw tangent at point P. Obviously there will be two tangents corresponding to two field lines. This means that at point P there exists two electric fields in two directions which is not possible. This is the reason, two electric filed lines can never intersect. Got it? Please comment.