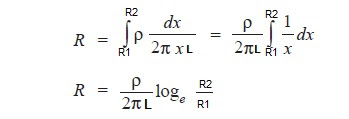It seems amazing that Insulation Resistance (IR) of a Cable is inversely proportional to the length of Cable. As per our general perception, the resistance is directly proportional to length of conductor but mind here that it is not the resistance of conductor rather it is the resistance of the Insulation provided around the conductor.
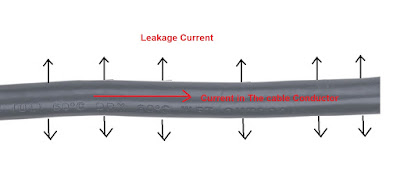
We can understand this by general thinking as, suppose there is a cable of length 100 m and it is having a insulation resistance of 500 Mohm. Now for this length of cable the leakage current will flow throughout the cable as shown in figure below. Here we are talking about leakage current because we are concerned with insulation resistance.
Now, if we cut the cable into two equal halves, then the leakage current through the insulation of cable will reduce by half as there is no full length of cable available for leakage current. Therefore, we can say that IR has increased two times i.e. to 1000 Mohm for our example.
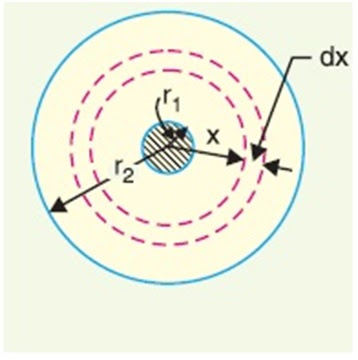
Now, we will see this aspect of insulation resistance mathematically. Consider a single core cable of radius R1 and internal sheath radius R2. Let L be the length of cable and ρ be the resistivity of the insulation.
For calculating the insulation resistance, we take an infinitesimally small layer of insulation of thickness dx at a radius R from the centre of the cable conductor. The length of insulation from where leakage current will flow is dx and area of cross-section will be 2πxL (A cylinder of length L and radius x).
Therefore,
Insulation Resistance (IR) of the assumed layer = ρdx/ 2πxL (From Resistance = ρL/A)
Now, for getting the IR of whole cable we need to integrate up to a radius of R2 starting from R1 and to a length L.
Insulation Resistance, R
Thus it is clear from the above expression that Insulation resistance is Inversely Proportional to the length of Cable.
Thank you!