The deflection of needle of moving iron instrument is given in terms of rms value of voltage or current. As the angular deflection of Moving Iron Instrument is proportional to square of operating current, therefore the instrument has basically square law response. Due to this square law response, the Moving Iron Instrument Scale is non-uniform.
If there were no saturation, the change of inductance with the angle of deflection i.e. dL/dƟ = constant and hence the instrument must have a pure square law response. For such pure square response, moving iron instrument scale can easily be graduated uniformly. But in actual instrument rate of change of inductance with angular deflection i.e. dL/dƟ is not constant rather it is a function of angular position of moving iron van. Due to this, moving iron instrument scale gets distorted from the square law response. This distortion in moving iron instrument scale can be controlled by suitable design i.e. by proper selection of dimension, shape and position of iron van. Thus it is possible to design an instrument having a scale which is very nearly uniform over a considerable part of its length.
Condition for Linear Moving Iron Instrument Scale
For moving iron instrument scale to be linear, current flowing through the stationary coil must be directly proportional to angular deflection i.e. I = CƟ where C is some constant. How am I saying this? It’s quite simple, if the scale is linear that means angular position of needle shall correspond to current (if we are measuring current).
As we know that the deflection of van of moving iron instrument is given as,
Ɵ = (1/2)(I2/K)(dL/dƟ)
Therefore,
dL/dƟ = (2KƟ) / I2
⇒ dL/dƟ = (2KƟ) / (CƟ) 2
⇒ Ɵx (dL/dƟ) = 2K/C2 = constant ………………..(1)
Thus from the above, the necessary condition for moving iron instrument scale to be linear is that product Ɵx (dL/dƟ) must be constant. Thus we got a design constraint for having linear scale.
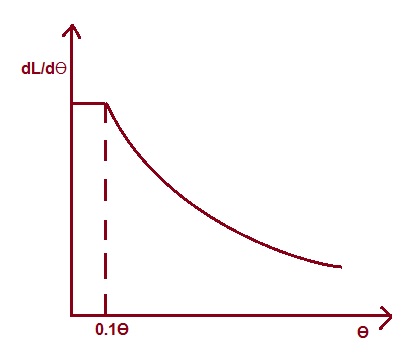
Now the question arises, can we have this product constant? This is not feasible at all. See when Ɵ is zero, (dL/dƟ) must be infinite which is not possible. In practice; moving iron instrument scale is made linear from maximum deflection down to 1/10th of the maximum deflection. In this range of linear scale, relationship between angular deflection and (dL/dƟ) is hyperbola as shown in figure below.
It is also possible to design and construct and instrument in which a small portion of the range, which is of importance is expanded over a large part while the remaining part is compressed into a relatively small space. It is quite clear form (1) that portion of moving iron instrument scale near zero can never be made uniform as it would demand to have infinite dL/dƟ.
In moving iron instrument, usually the scale is compressed or cramped at its lower and higher end. Thus the scale is almost uniform in between the lower and higher ends i.e. scale is usable over 80° of its length. Figure below shows a typical moving iron ammeter. Carefully observe that scale is compressed initially and readability starts from 10 to 15 degree approximately.
You may like to read,

"But in actual instrument rate of change of inductance with angular deflection i.e. dL/dƟ is not constant rather it is a function of angular position of moving iron van" here I believe that iron van is "Pointer" or "needle" or is it something else?
You are correct Ahmed. Your interpretation is correct, it is pointer connected with the van.
this is pointing device it means by pointer it show reading. is it more accurate than pmmc instrument?
The accuracy of instrument is dependent on its design and workmanship. Both PMMC instrument is suitable for measurement of DC quantity and Moving Iron instruments are suitable for both AC and DC. But due to hysteresis effect, an appreciable error is introduced in the measurement of DC by Moving Iron Instruments. Therefore, PMMC is more accurate than Moving Iron instrument. Hope it help you. Thank you!