Moving Iron Instruments are the most common type of ammeter and voltmeter used at power frequencies in laboratories. These instruments are very accurate, cheap and rugged as compared to other AC instruments.
Working Principle of Moving Iron Instruments:
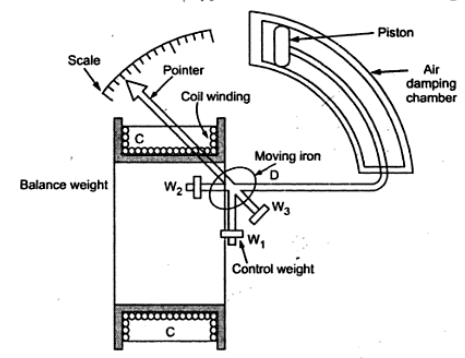
In Moving Iron Instruments, a plate or van of soft iron or of high permeability steel forms the moving element of the system. The iron van is so situated that it can move in the magnetic field produced by a stationary coil. Figure below shows a simple moving iron instrument.
The stationary coil is excited by the current or voltage under measurement. When the coil is excited, it becomes an electromagnet and the iron van moves in direction of offering low reluctance path. Thus the force of attraction is always produced in a direction to increase the inductance of coil. Mind that as the van follows the low reluctance path, the net flux in air gap will increase which means increased flux linkage of coil and hence inductance of coil will increase. It shall also be noticed that, the inductance of coil is variable and depends on the position of iron van.
Torque Equation of Moving Iron Instruments:
Suppose that, at any instant of time current flowing in the coil is I. Thus the energy stored in the coil in the form of magnetic field = (1/2)LI2.
As soon as the current changes to (I+dI), deflection in the pointer becomes dƟ resulting into change in inductance of coil from L to (L+dL). Let this deflection in pointer is due to deflection torque Td.
Thus mechanical work done = Tdx dƟ ………………..(1)
Energy stored in Coil = (1/2)(L+dL)(I+dI)2
Change in stored energy of coil
= Final Stored Energy – Initial Stored Energy
= (1/2)(L+dL)(I+dI)2 – (1/2)LI2
= (1/2)[ (L+dL)(I+dI)2 – I2L]
= (1/2)[ (L+dL)(I2+2IdI+(dI)2 – I2L]
= (1/2)[ LI2+2LIdI+L(dI)2 + dLxI2+2IdIxdL+dLx(dI)2 – I2L]
Neglecting second order and higher terms of differential quantities i.e. L(dI)2, 2IdIxdL and dLx(dI)2
= (1/2)[ 2LIdI+dLxI2]
= LIdI +(1/2)dLx I2 ……………………(2)
Again, just think, when there is a change of current from I to (I+dI), this change change of current must be accompanied by change in emf of coil. Thus we can write as
e = d(LI) / dt
= IdL/dt + LdI/dt
But electrical energy supplied by the source = eIdt
= (IdL + LdI) x I
= I2dL + LIdI
According to law of conservation of energy, this electrical energy supplied by the source is converted into stored energy in the coil and mechanical work done for deflection of needle of Moving Iron Instruments.
Hence,
I2dL + LIdI = Change in stored energy + Work done
⇒ I2dL + LIdI = LIdI +(1/2)dLx I2 + Tdx dƟ ….[from (1) and (2)]
⇒ Tdx dƟ = (1/2)dLxI2
⇒ Td = (1/2)I2(dL/dƟ)
Thus deflecting torque in Moving iron Instruments is given as
Td = (1/2)I2(dL/dƟ)
From the above torque equation, we observe that the deflecting torque is dependent on the rate of change of inductance with the angular position of iron van and square of rms current flowing through the coil.
In moving iron instruments, the controlling torque is provided by spring. Controlling torque due to spring is given as
Tc = KƟ
Where K = Spring constant
Ɵ = Deflection in the needle
In equilibrium state, deflecting and controlling torque shall be equal as below.
Deflecting Torque = Controlling Torque
⇒ Td = Tc
⇒ (1/2)I2(dL/dƟ) = KƟ
⇒ Ɵ = (1/2)(I2/K)(dL/dƟ)
From the above torque equation, we observe that the angular deflection of needle of moving iron instruments is square of rms current flowing through the coil. Therefore, the deflection of moving iron instruments is independent of direction of current.
I have need the type of electrical measuring instrument with principle