Hexadecimal Number System

This article explains the hexadecimal number system. Method to convert a hex to decimal, decimal to hex, hex to binary and binary to hex has also been elaborated with examples.

What is Hexadecimal Number System?

Hexadecimal number system is a system which uses 16 digits. Unlike decimal numbering system, this system uses digits 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E &F to represent a number. Digits A,B,C,D,E&F represents 10,11,12,13,14,15 and 16 respectively.

In Hexadecimal number system, each significant position has a positional weight. The least significant position has a weight of 16⁰ i.e. 1; the higher significant positions are given weights in the ascending powers of sixteen i.e. 16¹, 16², 16³ etc. respectively.

The hexadecimal equivalent of a decimal number can be obtained by dividing the given decimal number by 16 repeatedly until quotient of zero is obtained.

Decimal to Hex Conversion:

To convert a decimal number into Hex, the number is divided by 16 progressively till quotient zero is reached. The equivalent Hex for the given decimal is the remainders obtained in reverse order.

Let us consider an example to better understand decimal to hex conversion.

Example-1: Suppose, we need to convert (115)₁₀ into its equivalent Hex.

Division	Generated Remainder
16) 115
16) 7	3
16) 0	7

 

Reading remainders from bottom to top is the equivalent Hexadecimal number i.e. (73)₁₆ is the equivalent hex for decimal number 115.

Example-2: Suppose, we need to convert (235)₁₀ into its equivalent Hex.

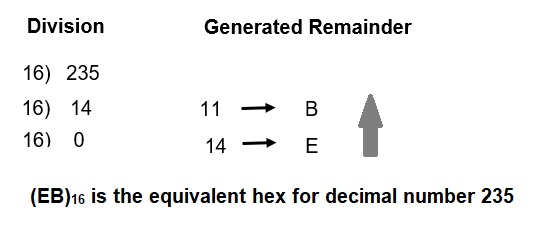
Reading remainders from bottom to top is the equivalent Hexadecimal number i.e. (EB)₁₆ is the equivalent hex for decimal number 235.

Hex to Decimal Conversion:

The conversion from a hex to decimal number can be carried out by multiplying each significant digit of the hex number by its respective weight and adding the products. This is illustrated in the following example:

Example-1: Convert hex (A3BH)₁₆ into equivalent decimal number.

A3BH

= Ax16²+3×16¹+Bx16⁰

= Ax256 + 3×16 + B

= 10×256 + 48 + 11

= (2619)₁₀ Answer

Hex to Binary Conversion:

Conversion from hexadecimal (hex) to binary and vice versa can easily be carried out. For arriving at the binary equivalent of a hex number, each significant digit in a given number is replaced by its 4-bit binary equivalent. Example shown below illustrate the process of conversion from hex to binary:

The binary equivalent of hex number (2D5)₁₆ is (001011010101)₂. Answer

Binary to Hex Conversion:

To convert a binary number into its equivalent hex number, a group of 4-bit is made starting from the least significant digit. Each group of 4-bit is then replaced by its equivalent hex number. Example below illustrate the process.

 

The hex equivalent is (7B5)₁₆. Answer