4 Most Asked Numerical Questions

In job interview often interviewer asks some numerical this is quit tricky and easy to answer without going into much calculation. In this post, I am going to discuss 3 most asked numerical questions in job interviews. These 3 questions are picked from my personal experience.

Question No. 1

Find the current flowing through the RLC circuit connected through an AC source of 240 V as given below. The values of R = 100 Ohm, L = 100 mH and C = 100 µF. (Assume frequency of source to be 50 Hz)

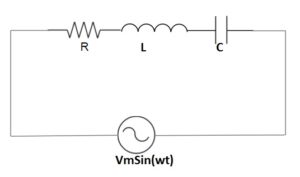
Solution:

In this question, the trick or point is that the inductive reactance and capacitive reactance are equal in magnitude.

Inductive Reactance X_L = ωL

                                        = 2πfL

                                        = 314x100x10^-3 Ohm

                                        = 31.4 Ohm

Capacitive Reactance X_C = 1/ωC

                                           =1/2πfC

                                        = 1/(314x100x10^-6)

                                        = 1/0.0314

                                        = 31.4 Ohm approx

Therefore the net impedance of the circuit Z

= R+jwL-j/wC = R = 100 Ohm

Hence, the circuit is pure resistive circuit and therefore the current flowing through the circuit will be

I = 240/100 Amp = 2.4 Amp. (Ans.)

Question No. 2

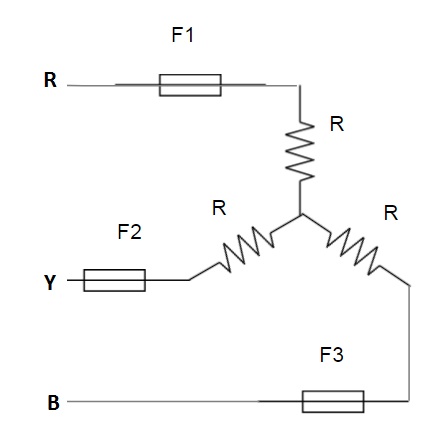
A balanced three phase load is connected to three phase supply 100 V(line), 50 Hz through Fuse F1, F2 and F3. If one of the fuse say F3 blows out then find the power consumed by the load. R = 10 ohm.

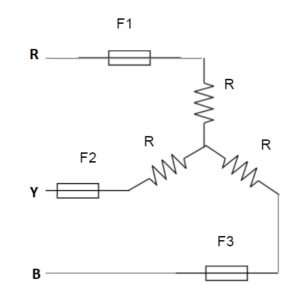
Solution:

Let us first calculate the phase voltage,

V_ph = V_line/1.732

       =  100/1.732

       = 57.74 Volt

Therefore, current flowing in the R phase is given as

I_R = 57.74/10 = 5.774 Amp

Hence, Power consumed in R phase load

P_R = (I_R)²R

      = (5.774)²x10 Watt = 333.4 Watt

Similarly

Current flowing in the Y phase

I_Y = 57.74/10 = 5.774 Amp

Hence, Power consumed in R phase load

P_Y = (I_Y)²R

      = (5.774)²x10 Watt = 333.4 Watt

Thus, the total power consumed in the load,

P = 333.4 + 333.4 = 666.8 Watt (Ans.)

You will think, what is different in this question? Actually many students making mistake by taking series equivalent of resistance i.e 20 Ohm and then find the current to calculate power consumed as below.

I = 100/20 = 5 Amp.

So power consumed P = 5²x20 = 500 Watt which is wrong.

Question No. 3

A parallel plate capacitor of plate area A is filled with dielectric of permittivity ε up to ‘d’ while the remaining gap ‘t’ is air. Find the equivalent capacitance.

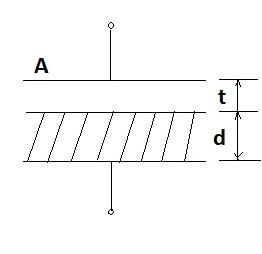
Solution:

The above arrangement can be think of two capacitors. One capacitor filled with dielectric and with separation d & other filled with air and separation t. Both thses capacitors are connected in series. Let

C₁ = Capacitance of capacitor filled with dielectric

C₂ = Capacitance of capacitor filled with air

Therefore,

C₁= εA/d

But ε = ε₀ε_r, hence

C₁= ε₀ε_rA/d

And C₂ = ε₀A/t

Equivalent Capacitance of the system

C = Series combination of C1 and C2

    = C₁C₂/(C₁+C₂)

    = (ε₀ε_rA/d)(ε₀A/t)/[ (ε₀ε_rA/d)+ (ε₀A/t)]

    = ε₀ε_rA / (ε_rt+d)

Thus,

Equivalent Capacitance = ε₀ε_rA / (ε_rt+d)

Question No. 4

Find the voltage across the capacitor terminal at time 1 ms for the circuit below.

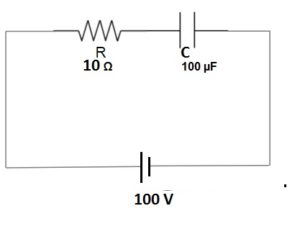
Solution:

This question seems easy and students apply the capacitor charging formula

V_c = V_o(1-e^-t/RC) where V_o = 100 V

So by using the above formula,

V_c = 100x(1-e^-1ms/RC)

Now, RC = 10x100x10^-6 = 1 ms

So, V_c = 100x(1-e^-1ms/1ms)

           = 100x(1-e^-1) Volt

As calculator is not allowed, so student end up to this calculation and leave the question.

But the thing to be noted that once you find the value of time constant RC, you should stop there and think that we are asked to find the voltage across the capacitor after 1 time constant i.e. 1 ms. We know that in one time constant the voltage across the capacitor is 63%.

Hence voltage across the capacitor terminal at t = 1 ms,

V = 63% of 100 V = 63 Volt (Ans)