Average Value of AC Current – Definition, Formula and Application

Definition

Average value of AC or alternating current is expressed by that DC current which transfers across any point of circuit the same charge as is transferred by the AC current for the same time.

This means, if AC current I in a circuit flows for t sec and charge Q is transferred across any point of circuit in this time t by this AC current then the same charge Q will also be transferred by its avg. current I_avg in the same time.

Calculation of Average Value of AC

Let us consider a sinusoidal current i = I_mSinωt as shown in the figure below. We will calculate its avg. value for one time period ωt = 2π from the definition of average value of alternating current.

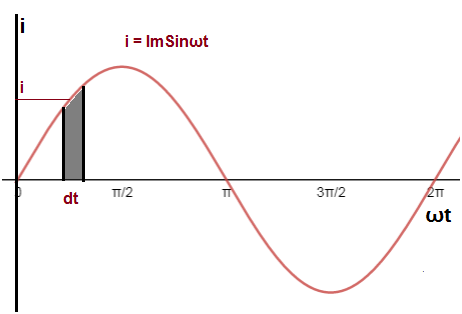
As per definition, we need to find the charge transferred by this AC current for time t = (2π /ω). For this, let us consider a infinitesimally small time interval dt where the value of current is i as shown in above figure. The charge transferred by this assumed current i in this time dt is given as

dq = idt  (Since i = dq/dt)

Now, we will integrate this for the entire time period i.e. from ωt = 0 to 2π to get the total charge transferred in one time period.

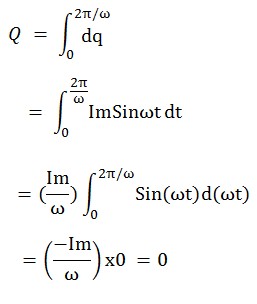
Thus, the charge transferred by AC current for one time period is zero. Therefore, its average value is zero. This can also be explained in other way. Since the positive and negative half cycles are equal, therefore the charge transferred due to these two halves will be equal but in opposite direction. Therefore, net charge transferred across any point of circuit in one time period of sinusoidal AC current is zero. Hence, its average value is zero. For this reason, average value of sinusoidal AC current or voltage is defined and calculated for half cycle i.e. for t= (π/ω). Let us now calculate this.

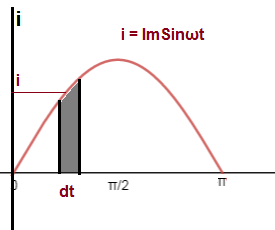
Charge Transferred across any point of circuit for half cycle is given as below.

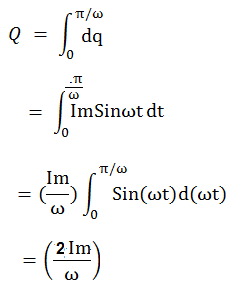
Thus the charge transferred by half cycle of Sinusoidal AC current = (2I_m/ω)

If I_avg being the average value, then this current must also transfer the same charge for t = (π/ω).Since average value is the DC value, this charge will be equal to Q = I_avgx(π/ω).

Thus,

I_avgx(π/ω) =  (2I_m/ω)

I_avg = (2I_m / π)

        = 0.637I_m

The average value of AC sinusoidal current or voltage is equal to 0.637 times of its peak value.

Formula of Average Value of AC Current or Voltage

From the above discussion, it must have been clear to the reader that, avg. value can easily be calculated by just using the basic concept. But we can have generalized formula to find out average value.  Average value of any periodic function with time period T is given as

The periodic function may either be ac current or voltage function. Thus, using this formula, we can find the avg. value of any ac current or voltage waveform.

Application:

Let us find the average value of output current of single phase half wave rectifier using the formula. The output current waveform of single phase half wave rectifier is shown below.

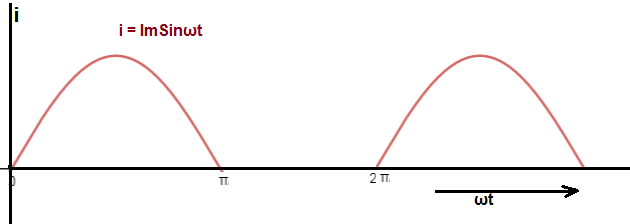
Let’s apply the formula. But for this, first of all we need to know the function and its time period. Here, the function is output current waveform which is defined as below.

 i = I_mSinωt for 0≤ ωt≤π

   = 0 for π ≤ ωt≤2π

The time period of this output current waveform is obviously 2π. So we are now fully equipped to find the average value of output current waveform of single phase half wave rectifier using formula. Let’s apply then.

 

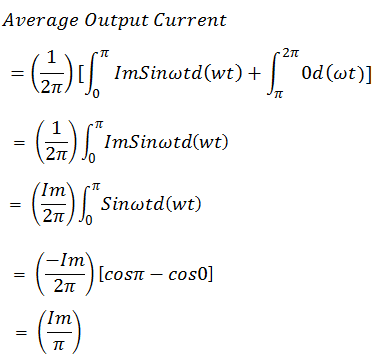
Thus, the average value of output current of single phase half wave rectifier is equal to its peak value divided by π i.e. (I_m/π). Similarly, the average value for full wave rectifier can also be calculated. In fact, the formula is general and can be used for any given function. This is a very important concept and one must understand how to apply the formula for getting its value. This is used very frequently in Power Electronics in rectifier circuit. Watch the video for a quick recap of the article and better understanding.

Hope, you fully understood the average value of AC quantities, its formula and above all how to apply it. Let me ask you one question. Is average value a DC quantity? Please write your answer in comment box.