Definition
Root Mean Square (RMS) value of AC current is defined as the steady or DC current which when flowing through a circuit for a given time period produces the same heat as produced by the AC current flowing through the same circuit for the same time period. RMS value is also known as effective value or virtual value of AC current.
Calculation of RMS Value
Suppose an AC current i = ImSinωt is flowing through a circuit and we are interested in calculating the rms or root mean square value of this current.
The root mean square or rms value can be calculated using two different methods: Mid-ordinate method and Analytical Method.
Both these methods can be conveniently used for rms value computation of symmetrical or non-symmetrical sinusoidal or non-sinusoidal waveforms. Mid-ordinate method is quite handy for symmetrical non-sinusoidal waveforms. Let us discuss each of the method one by one.
Mid-ordinate Method:
In mid-ordinate method, the time base of positive half of AC waveform is divided into n equal time intervals each of duration (T/n) second.
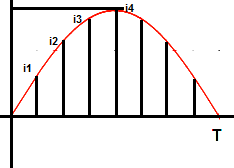
In the above figure, the entire positive half cycle is divided into n equal time intervals. You might ask why we only considered the positive half. This is because, as we are going to calculate the heat produced by the AC current, we need to apply I2R formula. Squaring current (I2) will make positive and negative cycle of symmetrical waveform equal. Therefore it will be wise decision to only consider the positive cycle.
Let us now proceed further to find the heat generated in the circuit due to flow of AC current waveform shown in above figure.
Heat produced in the 1st time interval = i12R(T/n) Joule
Heat produced in the 2nd time interval = i22R(T/n) Joule
………………………………………………………..
………………………………………………………..
Heat produced in the nth time interval = in2R(T/n) Joule
Thus the total heat produced by this current =
i12R(T/n) + i22R(T/n) + ……+ in2R(T/n) ……………(1)
Let the root mean square or rms value of this current is Irms. This current DC current Irms should generate heat Q equal to Irms2RT. Therefore as per the definition of rms current,
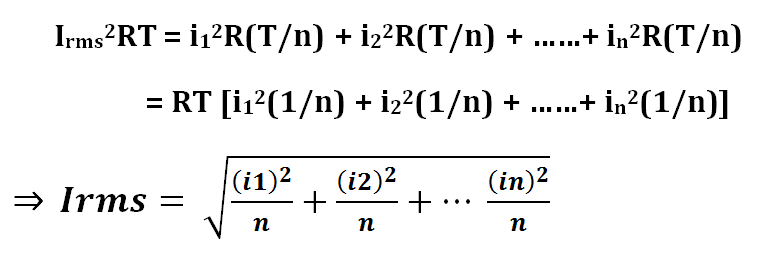
From the above expression of rms value, it is clear that rms value of AC current is equal to the square root of mean of the squares of the instantaneous current values. Though the above formula has been derived for AC current, it is well applicable for AC voltage too. The only difference will arise that, instead of taking instantaneous current values, instantaneous voltage value should be taken.
Analytical Method
I personally love this method for calculating the rms value of ac quantities. In fact, this method is not different from mid-ordinate method. In mid-ordinate method we calculated the rms value by considering the discrete values of instantaneous current at different time interval. But in analytical method, we use integration for getting the mean of the squares of the instantaneous current values and then find the square root of it to get rms value.
To calculate rms value, we need to first calculate the average value of square of AC current / voltage for one time period. Then we find the square root of calculated average value. This gives the root mean square (rms) value. That’s all we need to do.
Since the average value of any function f(x) having time period T is given by

Therefore, the average value of square of f(x),
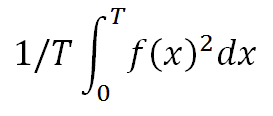
Therefore the formula for rms value is
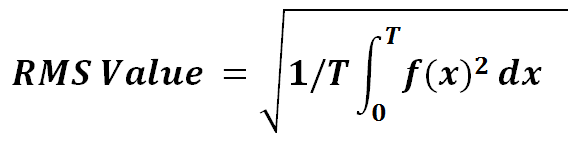
This formula for rms value calculation is very important and can be applied for any kind of waveform. I personally use this. I never use mid-ordinate method. I will recommend you to use this formula. Read “How to Find RMS value of any Function” to see how this formula can prove the ultimate weapon for rms value calculation.
RMS Value of Standard AC Sinusoidal Current
Well, all of us know that a standard AC sinusoidal current is written as i = ImSinωt. We are asked to find rms value of this current. How will you calculate? I will use analytical method or frankly the formula for rms value. Figure below shows the waveform of sinusoidal AC current waveform.
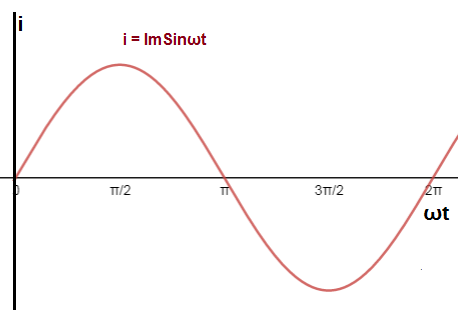

Step-1: Determine the time period T of waveform.
The time period T of the waveform is 2π as evident from its waveform.
Step-2: Use the formula.
For our example, we will put T = 2π and f(x) = ImSinωt in the formula.
RMS Value of sinusoidal AC current is calculated as below.
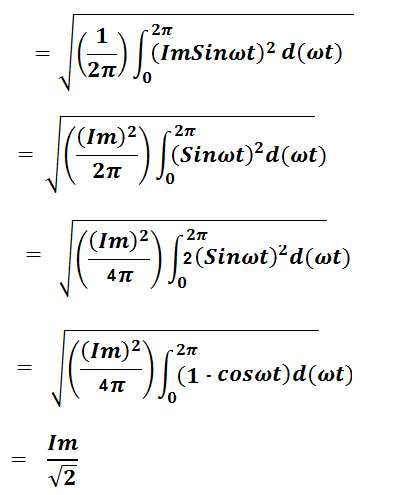
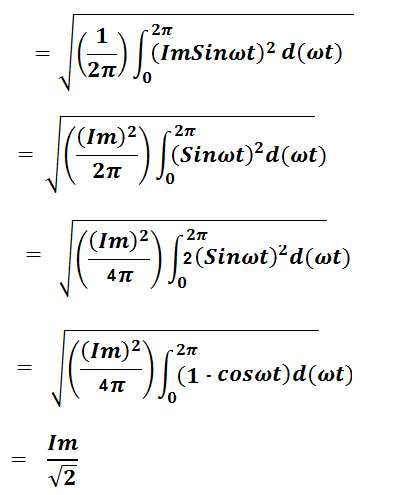
Thus, rms value of sinusoidal AC current or Voltage is equal to the peak value of current / voltage dived by √2.
RMS Value of Complex Wave
Let us consider a complex wave to illustrate the method or formula for calculating rms value. Suppose a current having equation i = A1Sinωt + A2Sin3ωt + A3Sin5ωt is flowing through a resistance R. Since this current is comprising of fundamental current component along with 3rd and 5th harmonic component, the heating effect of such complex current for one time period T will be due to the individual heating effect of fundamental as well as 3rd and 5th harmonic components.
Heating due to Fundamental Current = (A1/√2)2RT
Heating due to 3rd Harmonic Current = (A2/√2)2RT
Heating due to 5th Harmonic Current = (A3/√2)2RT
Hence, total heating by the complex current will be the sum of the individual heating effects of fundamental and 3rd & 5th harmonic current components.
If I be the root mean square (rms) value of the complex current, then the equivalent heating effect will be I2RT. But from the definition, this must be equal to the heating actually produced by the complex current. Therefore,


Hence for complex wave, the rule is as follows:
“The rms value of complex current or voltage wave is equal to the square root of the sum of the squares of the rms value of its individual components.”
RMS Value Formula
The formulas for rms value are tabulated below.
| Sr. No. | Nature of AC Waveform | Formula for RMS Value |
| 1) | Sinusoidal AC Current or Voltage having peak value Im or Vm | Im / √2 or Vm/√2 |
| 2) | Any function f(x) | 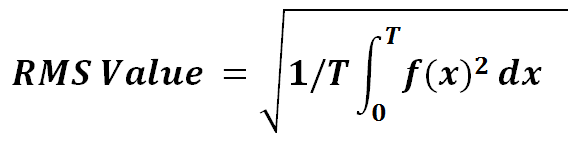 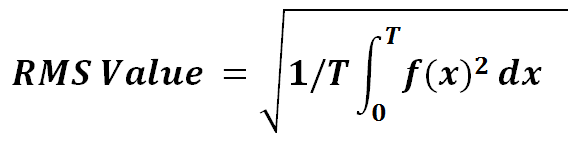 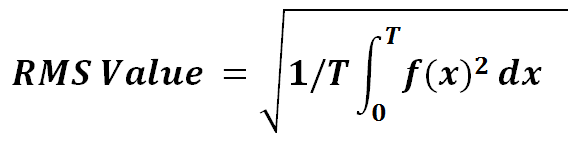 |
| 3) | Complex Wave | Square root of rms value of individual components |
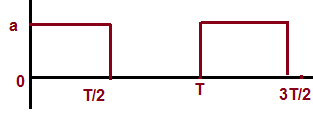
| 4) | Symmetrical Square Wave with amplitude ‘a’ and time period T.
|
‘a’ (equal to Amplitude ) |
| 5) | Unsymmetrical Square Wave with amplitude ‘a’ and time period T.
|
a/√2 |
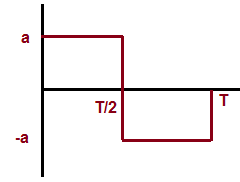
If our current is 120mA then what is rms value??
Please suggest us which is best meter for measuring mA AC rms.
Our maximum AC load current is 500mA.
Yokogawa micro ampere clamp meter having a measurement range of 10 amp is best suited. You can also look for Megger make.
Thanks