Initial value Theorem is a very useful tool for transient analysis and calculating the initial value of a function f(t). This theorem is often abbreviated as IVT. The limiting value of a function in frequency domain when time tends to zero i.e. initial value can easily be calculated using initial value theorem. This theorem can be written as,
where F(s) = Laplace Transform of f(t)
Let us now understand this theorem in detail. Initial Value of a function itself means the value of function near to zero. Mathematically we can say that Initial Value of function means limiting value of function when time tends to zero. This means,
Note that limiting value of f(t) is taken as f(0+) not f(0-). This is because the function is defined t≥0.
Proof of Initial Value Theorem:
So our target is to find f(0+).We know that Laplace Transformation of derivative of function f(t) involves f(0+), so we will try to use this to find f(0+). But the question arises that how to convert time into frequency? Well, since s = jw and w = 2πf = 2π/T hence when time tends to zero, s must tend to infinity.
We know that,
L[df(t) / dt] = [sF(s) – f(0+)]
Taking limit to both sides when s → ∞
But
From (1), we can write
|
Thus Initial Value of f(t) = lim sF(s)
s → ∞
|
Thus to apply IVT, first we need to find the Laplace transform of function and then use the theorem to het the initial value. But in case where initial value of function can easily be found in time domain, it is not wise to apply Initial Value Theorem. Let us have a look at some examples.
Example-1: A function in Laplace domain is given as
F(s) = 2/s -1/(s+3)
Find the initial value of this function.
Solution:
Since function is given in Laplace domain so we should apply IVT to get the initial value. First we will find sF(s).
sF(s) = 2 – s/(s+3)
= 2 – 1/(1+3/s)
Using Initial Value Theorem,
Example-2:
A function is given as
F(t) = Ae-αtsin(δt + Ø)
Find the initial value of this function.
Solution:
Here the function is given in time domain. So before applying IVT, first we will check whether its initial value can easily be calculated in time domain without using IVT.
Notice that, here we didn’t apply IVT to get initial value rather we calculated it using simple conventional method.
Hope you enjoyed the post and understood Intial Value Theorem. If you have any doubt or value addition, please write in comment box.


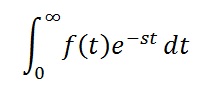
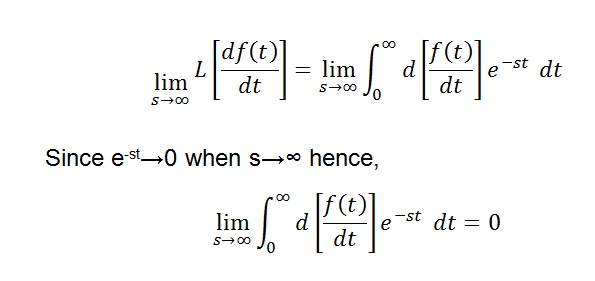
Beautifully explained the initial value theorem.