Statement of Maximum Power Transfer Theorem in AC Circuit:
In AC circuit, the maximum power transfer theorem is stated as: In a linear network having energy sources and impedances, the maximum amount of power is transferred from source to load impedance if the load impedance is the complex conjugate of the total impedance of the network. This means that, if source impedance is (R+jX) Ω, to have maximum power transfer, the load impedance must be (R – jX) Ω.
Explanation:
For better understanding of maximum power transfer theorem in AC circuit, let us consider a simple AC network as shown below.
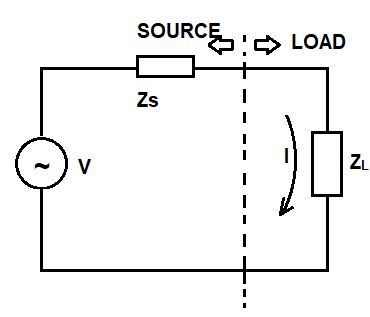
In this circuit, the source impedance is Zs whereas the load impedance is ZL. Let Zs = (R+jX). Then for delivery of maximum power from source to load, the value of load impedance should be conjugate of the source impedance. This essentially means that the value of ZL should be equal to (R – jX). This is maximum power transfer theorem for AC circuit.
Note that, in a DC circuit, the load resistance should be equal to source resistance, however, in AC circuit, load impedance is complex conjugate of source impedance.
Proof of Maximum Power Transfer Theorem in AC Circuit:
In this section, we will find the condition for delivery of maximum power from source to load in AC circuit and then will check, if the condition so obtained is in agreement with the theorem or not.
Let us consider the circuit shown above. Let us first find the current through flowing in the load impedance. Let ZL = (RL+jXL) and Z = (R+jX). The value of current is given as below.
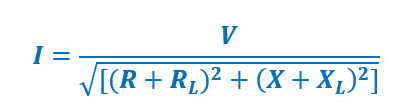
Now, we will calculate the power dissipated in the load. Since, no power is consumed by the inductance, therefore, the power dissipated in load is due to resistive part of its impedance. So, power will be dissipated in RL only. Let this power be PL.

The above expression gives the relationship in between the inductive part of impedance of source and load for maximum power transfer in an AC circuit / network. Let us put this value in the expression (1) of power dissipated in load impedance to get the value of PL. This shown below.
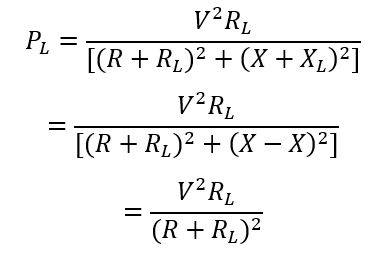
Now, to get the relationship between load resistance RL and source network resistance R for maximum power transfer from source to load, we will differentiate PL with respect to RL and equate it to ZERO. This is shown below.
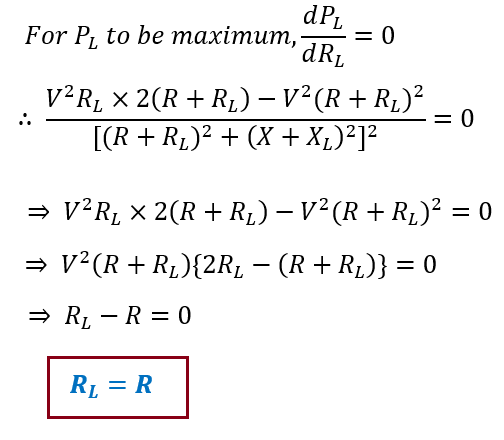
We see that the load resistance should be equal to the source network resistance. This is in agreement with the Maximum Power Transfer Theorem for DC circuit.
Therefore, we can say that, for maximum power transfer from source to load impedance in an AC circuit the necessary condition is that the value of load impedance should be equal to (R – jX) if the source impedance is (R+jX). Since (R-jX) is complex conjugate of (R+jX), we can say that, the value of load impedance must be complex conjugate of source network impedance. Thus, the maximum power transfer theorem in AC circuit is proved.
The amount of maximum power transferred may be find out by putting RL = R and XL = -X in information (1). This maximum amount of power delivered to load from source is (V2/4RL).