Voltage Division Rule – Explanation, Formula & Derivation

What is Voltage Division Rule?

Voltage Division Rule states that the total voltage applied across a series connection of multiple resistors is divided among the resistors in proportional to their resistance. This means, the voltage drop will be maximum across the resistor having maximum value of resistance. Likewise, it will be minimum for resistor having lowest value of resistance.

Voltage Division Rule basically tells us about the voltage drop across individual resistance in a series connected resistance. This rule is applicable for AC and DC circuit. However, while applying this rule in AC circuit, impedance value should be considered instead of resistance value due to obvious reason.

Explanation:

Let us consider the circuit below for better understanding. The circuit represents series connection of three resistors R₁, R₂ and R₃. The voltage across the terminals x-y is assumed V.

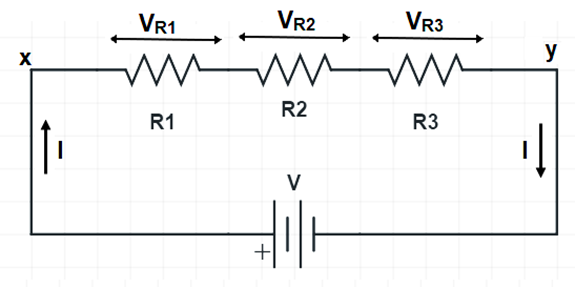
We want to find the voltage drop each of the resistances. Let V_R1, V_R2 & V_R3 be the voltage drop across resistance R₁, R₂ and R₃ respectively.

As per the statement of Voltage Division Rule, V_R1, V_R2 & V_R3 should be proportional to R₁, R₂ and R₃ respectively. Therefore, we can write

V_R1 = K R₁ …….(1)

V_R2 = K R₂ …….(2)

V_R3 = K R₃ …….(3)

But, total voltage V across terminal x-y must be equal to the sum of voltage drop across each of the resistances. Hence, we can write,

V = V_R1 + V_R2 + V_R3

Putting the value of V_R1, V_R2 & V_R3 from (1), (2) and (3), we get

V = K (R₁+ R₂+ R₃)

K = V / (R₁+ R₂+ R₃)

Using (1), (2) and (3) we can find the voltage distribution across the individual resistance as shown below.

V_R1 = V[ R₁/ (R₁+ R₂+ R₃)]

V_R2 = V[ R₂/ (R₁+ R₂+ R₃)]

V_R3 = V[ R₃/ (R₁+ R₂+ R₃)]

Though the above voltage distribution has been calculated assuming three number of resistors connected in series, the method is applicable for “n” number of series connected resistances in DC circuit and impedance in AC circuit.

Voltage Division Rule Formula:

The formula for voltage division rule for “n” number of series connected resistance is given below.

V_R1 = V[ R₁/ (R₁+ R₂+ R₃+……+ R_n)]

V_R2 = V[ R₂/ (R₁+ R₂+ R₃+……+ R_n)]

…………………………………………

V_Rn = V[ R_n/ (R₁+ R₂+ R₃+……+ R_n)]

Carefully observe the above formula. You will notice that, if we want to find voltage across any one of the resistances (say R₁), the total voltage (V) is multiplied with the ratio of another resistance (R₁) & total resistance (R₁+ R₂+ R₃+……+ R_n).

Derivation:

When a series combination of “n” number of resistances or impedances are connected to a source, the source voltage gets distributed among the resistances in such a way that the voltage drop across each of the resistance is in proportion with value of resistance. This is because, the current through all the resistance is equal (I) and hence voltage drop (V = IR) is only proportional to resistance.

Let us again consider the circuit shown earlier in the post. The voltage V impressed across the resistance is divided among the resistances. Current “I” is flowing in the circuit.

Therefore,

V_R1 = IR₁ …….(4)

V_R2 = IR₂…….(5)

V_R3 = IR₃…….(6)

Compare the information (3), (4) and (5) with information (1), (2) and (3) respectively. You will notice that, the proportionality constant “K” is the current “I” flowing in the circuit. Now, you may find the voltage V_R1, V_R2 & V_R3 in the same fashion as calculated earlier in the post.

Since, V = V_R1 + V_R2 + V_R3

Therefore,

V = I (R₁+ R₂+ R₃)

I= V / (R₁+ R₂+ R₃)

Using (4), (5) and (6) we can find the voltage distribution across the individual resistance as shown below.