Mutual Inductance
Mutual inductance is defined as inductance of a circuit caused by mutual coupling with other circuit. Mutual coupling of two coils means that magnetic field produced by one coil is linking / crossing the other coil and vice versa. Mutual Inductance is generally denoted by letter M and its SI unit is Henry.
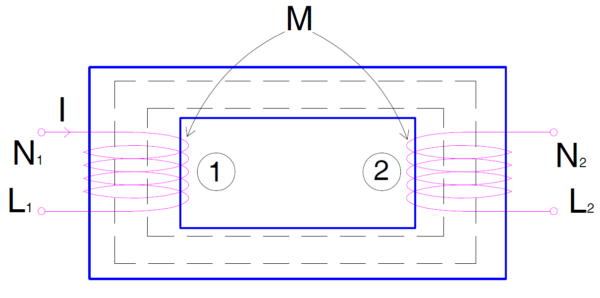
Let us take an example for better understanding of this mutual inductance. Suppose current I is flowing in one coil 1 and another coil 2 is kept in the vicinity of the coil so that their center are in a line.
Since the current in coil 1 is flowing in anticlockwise direction when viewed from Switch (S) side. Therefore as per Screw Law, magnetic field produced by the coil will be perpendicular to the coil 1 and toward the viewer. This magnetic field produced by the coil 1 will obviously link or pass through another coil 2. If this magnetic field is changing with time then flux through the coil 2 will change. Therefore, as per Faraday’s Law of Electromagnetic Induction an emf will be induced in the coil 2. This emf will be induced in such a way to oppose the cause i.e. changing magnetic field as per Lenz’s Law.
If magnetic flux Ø is linking with coil 2 then mutual inductance of coil 2 is given as
M2 = Ø / I …………………(1)
Now suppose battery and switch is connected to Coil 2 while keeping all other parameters like coil geometry, spacing etc. same. In this case magnetic flux due to coil 2 will also be Ø. This flux will link the coil 1 and therefore an emf will be generated in the coil. In this way, the mutual inductance of coil 1 will be given as
M2 = Ø / I …………………..(2)
From above two equation we see that, mutual inductance of both the coils are same if the geometry of coils are maintained. It shall be noted that mutual inductance only depends on the geometry like radius of coil, number of turns, spacing between the two coils etc like self-inductance.
Perfect Coupling or 100% Mutual Coupling
When entire magnetic field produced by one coil links or couples with the other coil then it is said that coupling between the coils is perfect or 100 % mutual coupling between the coils. But in actual there always exists some leakage of flux and therefore 100% or perfect mutual coupling is just a concept. Let us consider a simple circuit as shown in figure below.
The flux created by coil 1 having N1 number of turn is Ø. If leakage of flux is assumed zero, then the entire flux Ø will link with coil 2 having N2 turns. Therefore mutual inductance M21 of coil 2 is given as
M21 = Mutual Inductance of Coil 2 due to current in Coil 1
= Total Flux Linkage of coil 2 / Current in Coil 1
= N2 Ø21 / I1
But Ø21 = BA
Ø21 = [(µ0µrN1I1/L) x A] / I1
= µ0µrN1A/L
Therefore,
M21 = µ0µrN1N2A/L ………………….(3)
Now suppose same current I2 is flowing through coil 2 such that the flux produced by coil 2 is Ø (assuming cross-sectional area and length of both the coils are same). The mutual inductance of coil 1 is then given as
M12 = Mutual Inductance of Coil 1 due to current in Coil 2
= Total Flux Linkage of coil 1 / Current in Coil 2
= N1 Ø12 / I2
But Ø12 = Flux linking coil 1 due to magnetic field created by coil 2
= BA
⇒Ø12 = [(µ0µrN2I2/L) x A] / I2
= µ0µrN1N2A/L
Therefore,
M12 = µ0µrN1N2A/L ………………….(4)
From equation (3) and (4) we observe that, for perfect mutual coupling the mutual inductance of both the coils are same.
M12 = M21 = M = µ0µrN1N2A/L
Concept of mutual coupling is widely used in many electrical machines like Transformers, motors, generators etc.
Relationship between self-inductance and Mutual Inductance
Let the self-inductance of coil 1 is L1 and that of coil 2 is L2. Therefore
L1 = µ0µrN12A/L
L2 = µ0µrN22A/L
Multiplying the above, we get
L1L2 = (µ0µrN1N2A/L) x (µ0µrN1N2A/L)
= M x M
= M2
Thus for 100 % mutual coupling,
M2 = L1L2
Coefficient of Coupling or Coupling Factor
As discussed earlier in the post, perfect coupling or 100 % mutual coupling is just a concept. There is always some leakage of magnetic flux though we try to have minimum leakage possible. Therefore a fraction of magnetic flux generated by a coil only links with other coil. Due to this reason, coefficient of coupling or Coupling Factor came into picture.
Coefficient of coupling / Coupling Factor denotes the fraction of coupling or the fraction of flux linking the second coil due to flow of current in one coil. It is usually denoted by letter k. The value of k is given as
k = M / √(L1L2)
The value of k ranges from 0 to 1 i.e. 0 ≤k≤1
- If the value of k is 1 then the two coils are perfectly coupled or 100% coupling between them.
- If k>0.5, then the two coils are said to be tightly coupled.
- If k <0.5, the two coils or circuit is said to be loosely coupled.
| Type of Coupling | Value of Coefficient of Coupling (k) |
| Perfect Coupling | 1 |
| Tightly Coupled Circuit | >0.5 |
| Loosely Coupled Circuit | <0.5 |