Speed Control of DC Motor

DC Motor speed control means to have full control on the speed of DC Motor. The variation in speed of DC Motor because of variation in load is not the speed control. Therefore intentional variation in speed of DC Motor is called Speed Control.

As we know that for a DC Motor having armature resistance Ra, rotating at some speed ω_m,

V_t = E_a + I_aR_a  where E_a = Back EMF, I_a = Armature current and V_t = Supply Voltage

But E_a = K_aØω_m where K_a = constant = PZ/2πa so,

K_aØω_m = V_t – I_aR_a

Therefore, ω_m = Speed = (V_t – I_aR_a) /K_aØ       ………………………………(1)

From equation (1), it is clear that speed of a DC Motor can be controlled by the following methods:

• By varying the Armature circuit resistance

• By changing the field flux

• By varying the armature terminal voltage i.e. supply voltage.

We will discuss the first method of speed control i.e. by changing the Armature circuit resistance for DC Shunt Motor in this post.

Speed Control by Varying the Armature Circuit Resistance:

This method is called Armature Circuit Resistance Control method. In this method intentionally an external resistance is inserted in the Armature circuit of DC Motor. As an external resistance is added, hence there will be power loss in this resistance due to which the speed of DC motor will be less than its Name Plate speed or base speed.

Power input = Loss in External Resistance + Power Output of Motor, neglecting Motor losses.

So output power of DC Motor will reduce. Therefore, by Armature Circuit Resistance Control method only speed below base speed can be obtained.

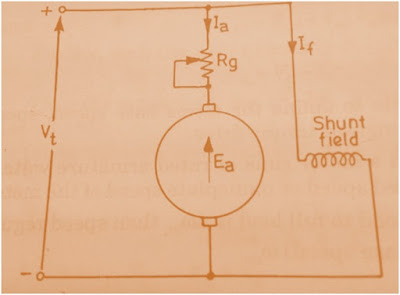
Speed Control of DC Shunt Motor by Armature Circuit Resistance Control Method:

The connection diagram for speed control of DC Shunt Motor using Armature Circuit Resistance Control method is shown in figure below. As shown in figure an External variable Resistance Rg is connected in series with the Armature circuit, called Controller.

               

Assuming a constant Torque drive, the torque requirement of the drive will be constant. But T_e = K_aØI_a so DC Shunt Motor will take constant armature current Ia to meet the constant torque requirement from the supply main as field flux Ø remain constant. 

Therefore Power delivered by the supply main to the DC Shunt Motor  = V_tI_a

But,

Power Delivered by Supply = I²(R_g+R_a) Loss + Output Power of DC Shunt Motor

V_tI_a = I²(R_g+R_a) +P_mo where P_mo = Motor Output

So, P_mo = V_tI_a – I²(R_g+R_a)

But P_mo = T_eω_m

So, ω_m = [V_tI_a – I²(R_g+R_a)] / T_e    ……………………..(2)

If we assume that no external series resistance has been connected to armature circuit and operating speed of DC Motor is ω_m0 then R_g = 0 and speed = ω_m0

Therefore from equation (2),

ω_m0 = (V_tI_a – I²R_a) / T_e ……………………………………(3)

From equation (2) and (3),

ω_m/ ω_m0 =   [V_tI_a – I²(R_g+R_a)] / (V_tI_a – I²R_a) <1

So, ω_m < ω_m0

Thus it is clear that speed of DC Shunt Motor reduces. As R_g is variable Resistor hence by changing this Resistance R_g we can have full control of speed of DC Shunt Motor. It is also clear that as we increase the value of External Series Resistor R_g, ohmic loss in this R_g will increase and hence the output of DC Motor will reduce which in turn will result in decreased speed.

It shall also be noted that as we increase the value of R_g, the efficiency of DC Shunt Motor will reduce as the output power of DC Motor is reducing.

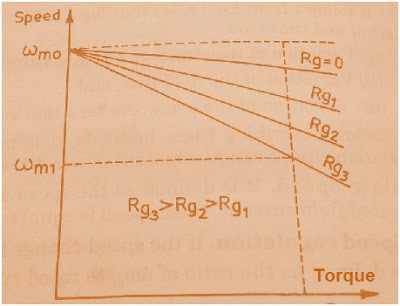
Speed Torque Characteristics of DC Shunt Motor for Different Value of R_g:

Assuming the no load speed of DC Shunt Motor = ω₀ and operating speed at a given Torque Te = ω_m1 then

So from equation (2) it is clear that we increase the value of External Series Resistance Rg, operating speed of DC Shunt Motor will decrease proportionally as shown in figure below.

Speed Control of DC Series Motor by Armature Circuit Resistance Control Method:

I will discuss this method for DC Series Motor by conventional way as you will find in most of the books but you can proceed in the same way as discussed for DC Shunt Motor.