Thevenin’s Theorem is the most used and useful approach to solve electrical networks. This is not a new way or approach rather it’s the same conventional way what we use to solve electrical networks but in an organized manner. Let me explain why this is not new.
If you are given an electrical network and asked to find the current through the load then obviously using conventional way, we are supposed to first find the voltage across the load and then divide this voltage by load resistance to get the current. This can also be said in different way, like we first we define the source to which the load is connected and then find the current. Now, source can be defined either by a constant current source or by constant voltage source. Mind that source resistance is connected in parallel in case of constant current source and in series in case of constant voltage source. Thus load may be supposed to be either connected by a constant voltage source or current source while solving electrical networks. This gave rise to two approaches which we often call theorem. In one approach, the load is assumed to be connected through a voltage source with source internal resistance connected in series. This approach is called Thevenin Theorem.
In second approach, the load is assumed to be connected through a current source with source internal resistance connected in parallel. This approach is called Nortan’s Theorem. So how the two approaches are new? Really they are not. But they are really organized and defined way. Let us discuss the first approach i.e. Thevenin’s Theorem.
Thevenin’s Theorem:
Thevenin’s Theorem states that any two terminal bilateral circuits can be replaced by an equivalent circuit having a voltage source and source resistance connected in series. This series resistance is often called Thevenin Resistance.
Bilateral circuit means that current can flow in either direction unlike diode where current can only flow in one direction. Therefore, diode is unilateral device whereas resistor is a bilateral device. So mind the limitation of Thevenin’s Theorem, it is only applicable for two terminal bilateral circuit.
Illustration
Let us consider the circuit below. Suppose we need to replace this circuit by thevenins equivalent circuit to find the current flowing through load rL.

To apply thevenins theorem, follow the following steps:
Step-1: Calculation of Open Circuit Voltage
First of all remove the load rL and find the open circuit voltage Voc as shown below.
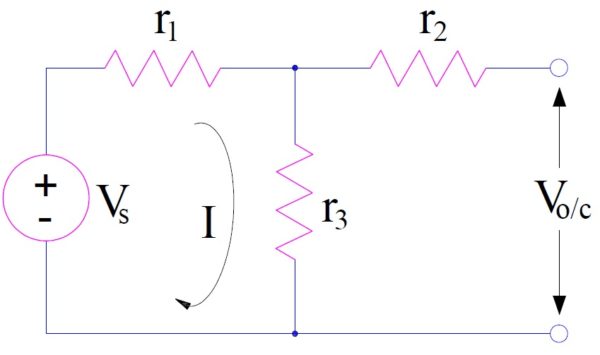
Open circuit voltage Voc will be equal to the voltage across the resistance r3. Hence,
Voc = r3I
= r3[Vs/(r1+r3)]
Step-2: Calculation of Thevenin Resistance
Look into the network from the open terminal to find the internal resistance i.e. thevenin resistance. There are some important points here to note and remember while calculation internal resistance. They are as follows:
Replace independent voltage source by its internal resistance. If the source is ideal voltage source, then short the source terminals.
If the network have constant independent current source, replace it by an open circuit.
In case the circuit contain dependent source, then to find thevenin resistance we can use either of two methods mentioned below.
Method-1:
First find the open circuit voltage Voc using conventional network analysis and then short the open terminals. Find the current through the shorted terminals Isc. The thevenin resistance = Voc/Isc.
Method-2:
Apply a dc voltage Vdc across the open terminals. Replace all the independent voltage source by short circuit and current source by open circuit and then find the dc current idc flowing into the circuit due to application of dc voltage Vdc. Thevenin Resistance is then given as
Rth = Vdc/Idc
Since the circuit in our example only have independent voltage source Vs, we will replace it by a short circuit to calculate thevenin resistance as shown below.
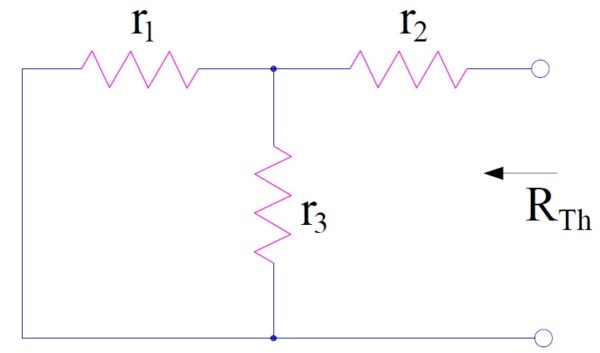
Thevenin Resistance Rth is equal to the equivalent resistance of network when viewed from open terminal. Hence,
Rth = r2 + (parallel equivalent of r1 and r3)
= r2 + r1r3/(r1+r3)
= (r1r2+r2r3+r3r1) / (r1+r3)
From step-1 and step-2, we can define the voltage source by its open circuit voltage and internal resistance (equal to thevenin resistance). Therefore in the Thevenin equivalent circuit, load rL will be connected to the defined source as below.
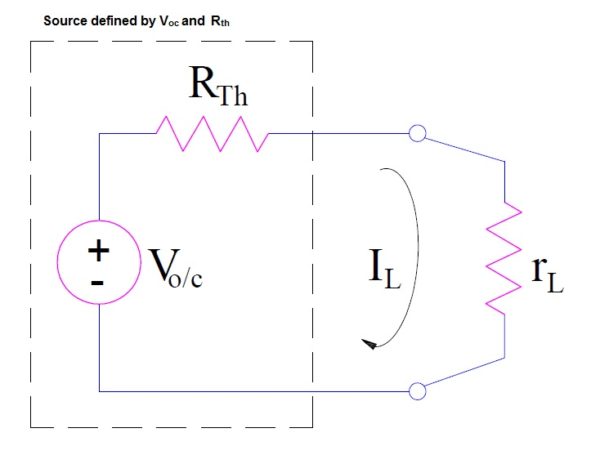
To have better understanding, let us discuss some examples.
Example-1:
In the circuit given below, find the current through resistance 5 Ω.
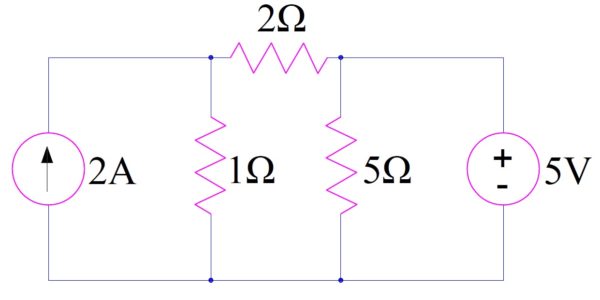
Solution:
Step-1: Calculation of open circuit voltage Voc.
Remove resistance 5 Ω. Find the open circuit voltage Voc by conventional method.
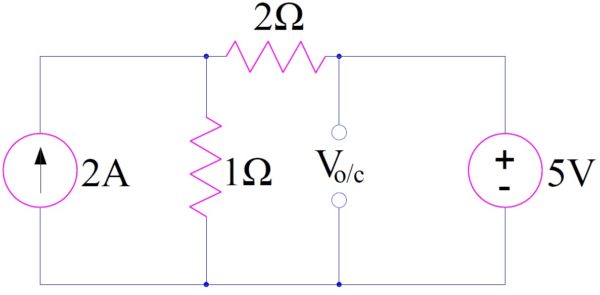
From the above figure, it is quite obvious that Voc = 5 V
Step-2: Calculation of thevenin resistance Rth.
Since the above circuit contains constant current source as well as constant voltage source, therefore to find thevenin resistance, we will replace them by open circuit for current source and short circuit for voltage source. This is shown below.
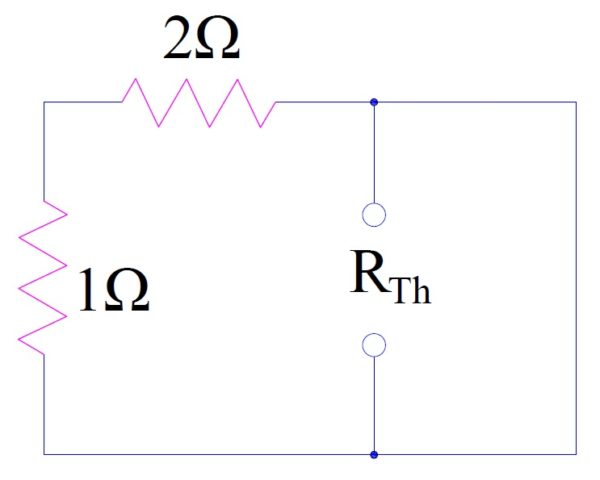
Thevenin Resistance Rth is equal to the equivalent resistance of network when viewed from open terminal. Hence,
Rth = parallel equivalent of [(1+2) Ω = 3 Ω] and 0
= 0
Hence the thevenin equivalent circuit will be as below.

From the above equivalent circuit, the current I flowing through resistance 5 Ω is given as
I = Vov/5 = 5/5
= 1 Amp. (Ans.)
Example-2:
Find the current through RL using Thevenin’s Theorem in the circuit below. Provided r = 5 Ω, RL = 10 Ω, v0 = 10 V and i0 = 2 A.
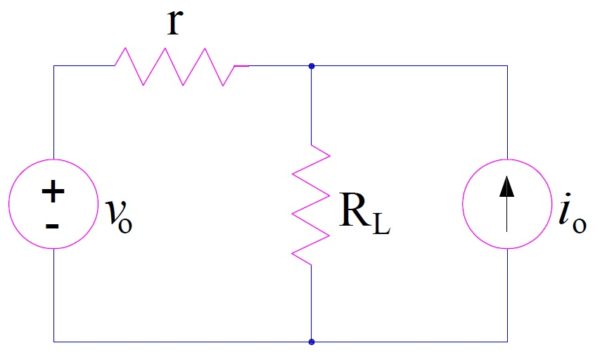
Solution:
Step-1: Remove RL and find open circuit voltage Voc as below.
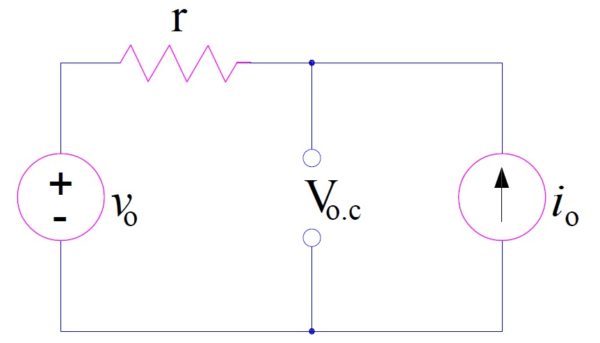
Voc = ri0 + v0
= (5×2 + 10) V = 20 V
Step-2: Find thevenin resistance by replacing current source and voltage source by open circuit and short circuit respectively and looking into the network through open terminals. This is shown in figure below.

Hence, Rth = r
Thus the thevenin equivalent circuit will be as below.
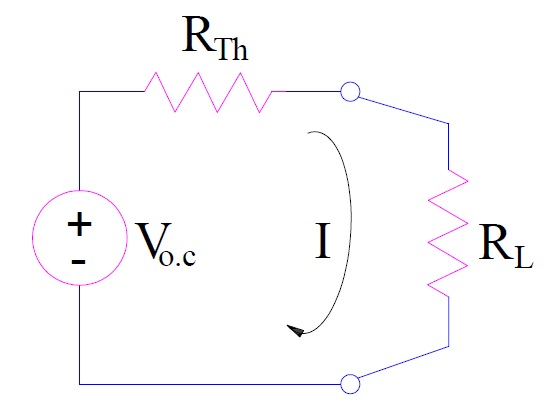
Thus the current through RL
= Voc/(Rth+RL)
= 20 / (5+10)
= 1.33 A (Ans.)
Thank you so much!
Excellent – well done!