Y Parameter of Two Port Network

Y parameter of two port network is a 2×2 admittance matrix. Since admittance is the ratio of circuit current and voltage, therefore this admittance matrix gives the relationship between the input and output current and voltage of the network. It is also known as short circuit admittance parameter.

The Y parameter for a two port network is defined as

[ I ] = [ Y ] [ V ]

where [ Y ] is the admittance matrix, [ I ] and [ V ] are the current and voltage matrix.

From the above matrix form representation of two port network, it is clear that there are four admittance parameters i.e. Y₁₁, Y₁₂, Y₂₁ and Y₂₂. Each of them has a special meaning and significance which will be discussed latter in this post.

Calculation of Y Parameter:

Let us consider a two port network. Let V₁, I₁, V₂ and I₂ are the input voltage, input current, output voltage and output current respectively.

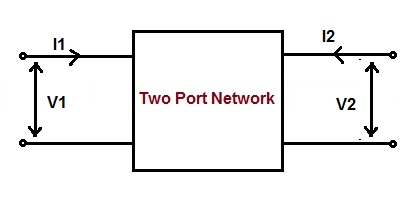
The relationship between the input and output quantities for the above network is obtained using (1) as below.

I₁ = Y₁₁V₁ + Y₁₂V₂ ……(2)

I₂ = Y₂₁V₁ + Y₂₂V₂ …….(3)

Assuming the output of the two port network to be short circuited, therefore

V₂ = 0

Now putting V₂ = 0 in (2), we get

I₁ = Y₁₁V₁

Y₁₁ = (I₁ / V₁)

Similarly putting V₂ = 0 in (3), we get

I₂ = Y₂₁V₁

Y₂₁ = (I₂ / V₁)

Again assuming input port of the two port network to be short circuited, the input voltage will be zero. 

V₁ = 0

Now putting V₁ = 0 in (2), we get

I₁ = Y₁₂V₂

Y₁₂ = (I₁ / V₂)

Similarly putting V₁ = 0 in (3), we get

I₂ = Y₂₂V₂

Y₂₂ = (I₂ / V₂)

Thus there are four Y parameter for a two port or four terminal network. Their values are tabulated below.

Y11	(I1 / V1)	Condition: Output port of the two port network is short circuited i.e. V2 = 0
Y21	(I2 / V1)
Y12	(I1 / V2)	Condition: Input port of the two port network is short circuited i.e. V1 = 0
Y22	(I2 / V2)

Significance of Different Y Parameter:

• Since Y₁₁ is the ratio of input current and voltage when the output port is short circuited, therefore it is known as input driving point admittance.
• Y₂₂ is the ratio of output current and voltage when input port is short circuited, therefore it is called output driving point admittance of the network.
• Y₁₂ is the ratio of input current and output voltage when input port is short circuited, therefore it is called reverse transfer admittance.
• Y₂₁ is the ratio of output current and input voltage when output port is short circuited, therefore it is called forward transfer admittance.

Equivalent Circuit Representation of Y Parameter:

The equivalent circuit of Y parameter for two port network can be represented using (2) and (3) as shown below.

In the above circuit, the current sources Y₁₂V₂ and Y₂₁V₁ are called Voltage Controlled Current Source.

Y Parameter Solved Problems:

To better understand the discussed concept of Y parameter, we will consider one example.

Example:

Find the Y parameter for the π circuit given below.

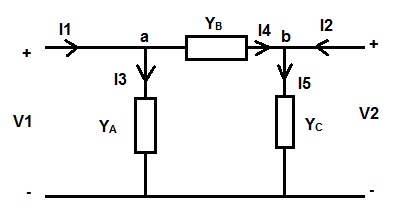
Solution:

Applying Kirchoff’s Current Law at node ‘a’,

I₁ = I₃ + I₄

    = V₁Y_A + (V₁ – V₂)Y_B

    = (Y_A + Y_B)V₁ + (-Y_B)V₂

Thus, I₁ = (Y_A + Y_B)V₁ + (-Y_B)V₂

But from (2),

I₁ = Y₁₁V₁ + Y₁₂V₂

Comparing the above two expressions, we get

Y₁₁ = (Y_A + Y_B)

Y₁₂ = -Y_B

Again, applying Kirchoff’s Current Law at node ‘b’

I₂ = I₅ – I₄

    = Y_CV₂ – (V₁ – V₂)Y_B

    = (-Y_B)V₁ + (Y_B + Y_C)V₂

Thus,

I₂ = (-Y_B)V₁ + (Y_B + Y_C)V₂

But from (3),

I₂ = Y₂₁V₁ + Y₂₂V₂

Comparing the above two expressions, we get

Y₂₂ = (Y_A + Y_B)

Y₂₁ = -Y_B

Hence, the four Y parameters are

Y₁₁ = (Y_A + Y_B), Y₁₂ = -Y_B, Y₂₂ = (Y_A + Y_B), Y₂₁ = -Y_B  (Answer)