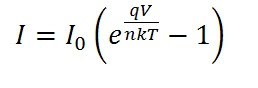Current through an Ideal Diode:
The diode equation gives an expression for the current through a diode as a function of voltage. The Ideal Diode Law, expressed as shown below
Where,
I = the net current flowing through the diode
I0 = Reverse Saturation Current
V = applied voltage across the terminals of the diode
q = absolute value of electron charge
k = Boltzman’s constant and
T = absolute temperature (K).
The Reverse Saturation Current (I0) is an extremely important parameter which differentiates one diode from another. I0 is a measure of the recombination in a device. A diode with a larger recombination will have a larger I0.
Note that,
I0 increases as T increases and
I0 decreases as material quality increases.
At 300K, kT/q = 25.85 mV, called Thermal Voltage.
Current through Non Ideal Diodes:
For actual Diodes, the expression becomes,
Where,
n = ideality factor, a number between 1 and 2 which typically increases as the current decreases.
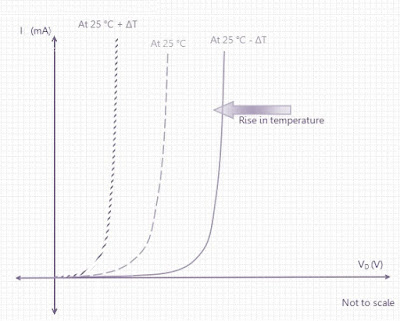
Effect of Temperature on Forward Characteristics of Diode:
The characteristics curve of a Si diode shifts to the left at the rate of -2.5 mV per degree centigrade change in temperature in forward bias region.
As shown in the graph above the curves at different temperatures are shown far apart just for illustration purpose. The curve shifts to the left at the rate of -2.5 mV per degree centigrade change in temperature. Hence if the temperature increases from room temperature (25° C) to 80° C, the voltage drop across the diode will be (80-25) x 2.5 mV = 137.5 mV.
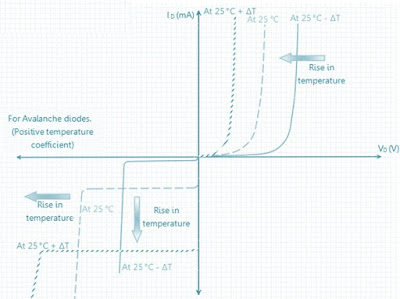
Effect of Temperature on Reverse Characteristics of Diode:
In the reverse bias region, the reverse saturation current of Si and Ge diodes doubles for every 10° C rise in temperature. Suppose an increase of temperature from 25 °C to 85 °C, where the reverse saturation current at 25 °C is 100 nA. The temperature increases by 60 °C (25 °C to 85 °C), which is 6 x 10. Hence the reverse saturation current would increase by a factor of 26 = 64. Hence the reverse saturation current at 85 °C will be 100 nA x 64 = 6400 nA.
A graph showing the variation of reverse saturation current with temperature is shown below.
From the above graph it is clear that the reverse saturation current increases with increase in temperature. The graph also shows how the reverse breakdown voltage changes with temperature. It is indicated in the above graph that the reverse breakdown voltage increases with an increase in temperature. However it is only true for avalanche diodes. The reverse breakdown voltage for Zener diodes decreases with an increase in temperature.