What is Current Division Rule?
Current Division Rule states that the total current divided into either of the parallel combination of two resistance or impedance is inversely proportional to the value of resistance / impedance. It basically tells us how the current is divided in the parallel connected resistance. This rule is applicable for AC and DC circuit. However, this rule should not be applied when the number of resistances in parallel is more than two.
Explanation:
Let us consider the circuit below for better understanding. In this circuit the total current I is getting divided into two resistances R1 & R2. I1 and I2 being the current through R1 and R2 respectively.
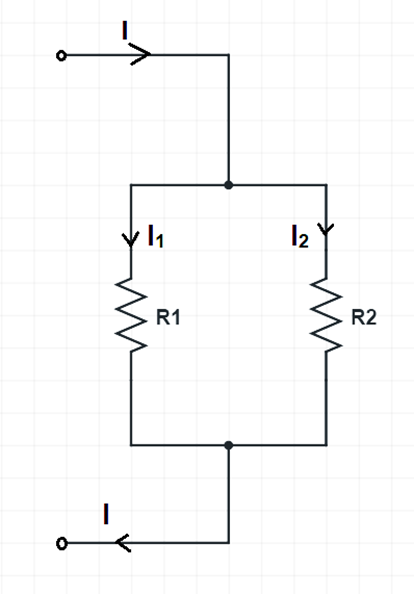
As per current division rule, the current I1 & I2 will be inversely proportional to R1 and R2 respectively. This means,
I1 = K/R1 …….(1)
I2 = K/R2 …….(2)
where K is constant of proportionality.
But total current I is getting divided into I1 and I2. This simply means,
I = I1 + I2
Therefore,
I = K (1/R1 + 1/R2)
So, K = I x [(R1 R2) / (R1+ R2)]
From information (1) and (2),
I1 = Ix[R2/(R1+R2)]
I2 = Ix[R1/(R1+R2)]
Current Division Rule Formula:
The formula for current division rule may be written as below.
I1 = Ix[R2/(R1+R2)]
I2 = Ix[R1/(R1+R2)]
Carefully observe the above formula. You will notice that, if we want to find current through any one of the resistances (say R1), the total current (I) is multiplied with the ratio of another resistance (R2) & total resistance (R1+R2).
Derivation:
When a parallel combination of two resistances or impedance are connected to a source, the current in the gets divided into two paths. The value of current in each path or resistance depends on the value of resistance. The more the resistance, the lesser will be the current. This is because, the voltage across the parallel combination of resistance is same, hence the current will be divided into each of the resistance as per Ohm’s Law.
Circuit below shows a parallel combination of resistance R1 & R2. Current through R1 and R2 are I1 & I2 respectively and the voltage drop across the combination is V. Total current is I. We are interested in calculating the value of current I1 & I2.

Since, the voltage across R1 is V, hence as per Ohm’s Law,
I1 = V/R1 …….(3)
Similarly, current through R2 is calculated as below.
I2 = V/R2 …….(4)
Compare the information (3) and (4) with information (1) & (2) respectively. You will notice that, the proportionality constant is the voltage V across the combination of resistances. Now, you may find the current I1 & I2 in the same fashion as calculated earlier in the post.
Since, I = I1 + I2
Therefore,
I = V (1/R1 + 1/R2)
So, V = I x [(R1 R2) / (R1+ R2)]
From information (3) and (4),
I1 = Ix[R2/(R1+R2)]
I2 = Ix[R1/(R1+R2)]
Thus, the total current is divided in the inverse ratio of resistance or impedance in a parallel connected resistances / impedances. This is current division rule.