Norton’s Theorem states that any linear bilateral circuit consisting of independent and or dependent sources viz. voltage and or current sources can be replaced by an equivalent circuit consisting of a current source in parallel with a resistance. The current source is the short circuit current across the load terminals and the resistance is the internal resistance when viewed from the open load terminals. This theorem can be applied to both AC as well as DC circuit.
Basically, Norton’s Theorem is the converse of Thevenin’s Theorem. Both the theorems tell us to about the method to a linear bilateral circuit into an equivalent circuit consisting of source and load. In both the theorems we need to find the internal resistance of circuit. The method of calculation of internal resistance is same for both the theorems.
The difference between the Norton’s and Thevenin’s theorem lies in equivalent source. It is a current source for Norton’s equivalent circuit whereas it is voltage source for Thevenin’s equivalent circuit. Another difference is the connection of internal resistance of circuit with the source. In Norton’s equivalent circuit, it is connected in parallel with the current source whereas in Thevenin’s equivalent circuit, it is connected in series with the voltage source.
Explanation of Norton’s Theorem:
To better understand the concept of Norton’s Theorem, let us consider a circuit as shown below.
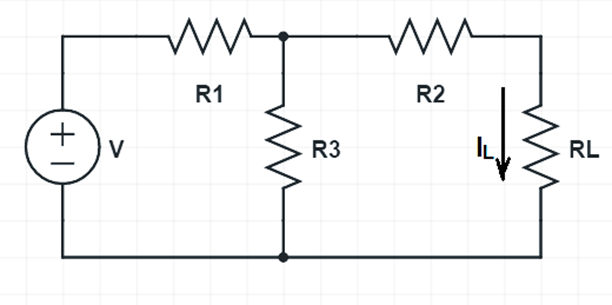
For the above circuit, we will try to find the Norton’s equivalent circuit. As the very first step, we will short circuit the load resistance RL and find the short circuit current Isc. Figure below depicts this step.
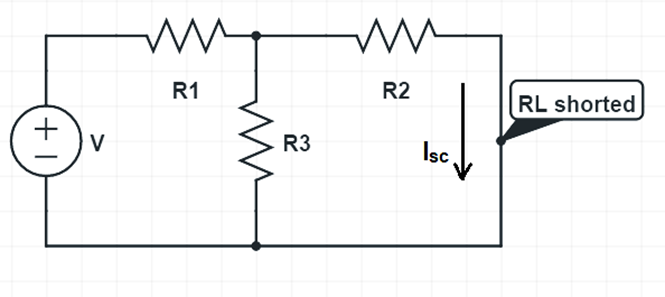
Let us now find short circuit current Isc using conventional circuit analysis. The is calculated as shown below.
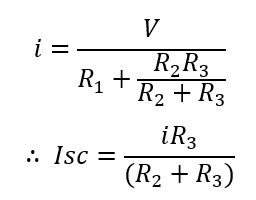
This current Isc is the magnitude or strength of current source of Norton’s equivalent circuit. Let us now find the internal resistance of the circuit. The main thing which should be taken care while calculating internal resistance is to replace current source by open circuit and voltage source by a short circuit. Also, keep the load terminals open and find the internal or equivalent resistance of circuit from open load terminal once you replaced all the sources. We will adopt this method.
Since, our circuit is only having a voltage source, we will replace it by a short circuit as shown below.
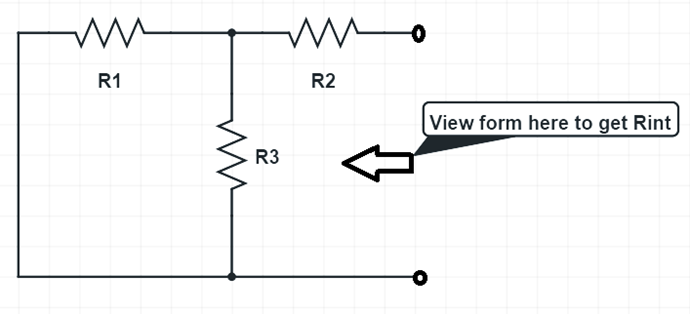
Let us call internal resistance Rint. Therefore, Rint is the series equivalent of R1 and parallel equivalent of R2 & R2.
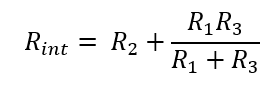
This Rint is the value of resistance which is to be connected in parallel with the current source Isc calculated earlier. Well, it’s time to draw the Norton’s equivalent Circuit.
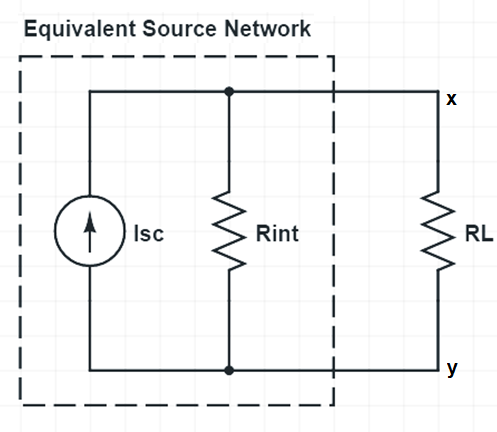
Norton’s Equivalent Circuit:
To draw Norton’s Equivalent Circuit, we connect current source Isc in parallel with internal resistance Rint. This connection is called equivalent source network. The terminals x-y of equivalent source network is then wired to load resistance RL to get the Norton’s equivalent circuit. This equivalent circuit is shown below.
While explaining Norton’s Theorem, I have already mentioned the steps to be followed to get the equivalent circuit. Further, an example is solved. This will make your concept of Norton’s Theorem as well as steps for solving problem very clear. Therefore, there is no need of separately mentioning the steps. In case you want us to elaborate the steps, kindly write in comment box.
Example:
Find the Norton’s equivalent circuit to the left of terminal x-y in the shown below.
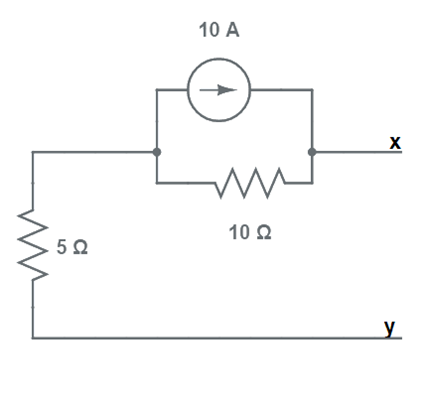
Solution:
Step-1: Short the terminals x-y as shown in figure below. Then, find the short circuit current Isc using conventional circuit analysis.
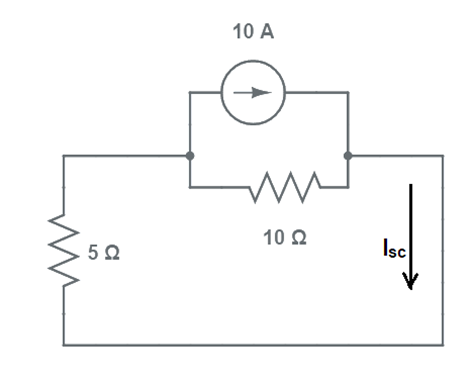
Carefully observe the above circuit. You will see that, 10 Ω and 5 Ω resistances are connected in parallel and current source of 10A is feeding this parallel combination. Short circuit current Isc is the current flowing through 5 Ω resistance. So, we can use current division rule to get this current as shown below.
Isc = (10×10) / (10+5)
= 6.67 A
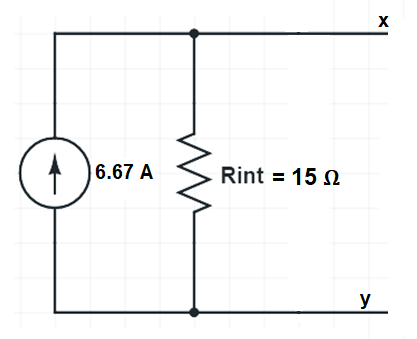
This current of 6.67 is the strength of current source of the Norton’s equivalent circuit.
Step-2: Find the value of internal resistance of circuit when viewed from terminal x-y. We will replace the current source by open circuit to get the internal resistance.

Internal Resistance Rint = 15 Ω
Step-3: This is the last and final step to convert a circuit into its Norton’s equivalent. In this step, we will connect 6.67 A (calculated in Step-1) current source in parallel to 15 Ω (calculated in Step-2) resistance. This gives Norton’s equivalent circuit. This is shown in figure below.
Hope you enjoyed the post. If you have any doubt / feedback, kindly write in comment box.