Definition
Distribution factor is defined as the ratio of phasor sum of coil emfs to the arithmetic sum of coil emfs. It is also known as Belt or Breadth factor and denoted by kd.
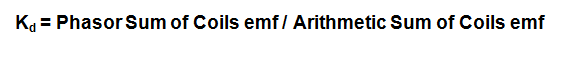
In electrical machine, armature winding is distributed in the slots. It is not concentrated in a single slot. Therefore the total emf generated across the armature terminal is the phasor sum of emfs induced in individual coils. If these coils were concentrated, then the total induced emf would have been arithmetic sum of induced emf in a single turn of coil. Thus to find the factor of distribution or the degree of distribution of coils, distribution factor has been defined as the ratio of emf induced in distributed winding to the emf induced in concentrated winding. This definition of distribution factor is same stated earlier in the post.
Calculation of Distribution Factor
To get a general expression or formula of distribution factor, let us assume a 2 pole, 3 phase electrical machine having a total of 18 slots in its stator. These slots are distributed along the periphery of stator in 2 pole pitches. Therefore the angle between any two consecutive slots will be equal to 20 degree (2×180 / 18 = 20). This angle between two consecutive slots is called Angular Slot Pitch. It is in electrical degree not in mechanical degree.
![]()
Thus angular slot pitch for our example is 20 degree. The number of slots per pole per phase will be 3 [(18/2)/3 = 3]. This means that a particular phase will consists of three coils distributed in three slots under a single pole. This is shown in figure below.

In the above figure it can be seen that, coils are distributed in slot number 1,2,3 and 10,11,12. It can also be observed that, coil sides are connected in series in such a way that emf induced in coil side at 1 and 10 are additive. This means, if E1 and E10 are the emf induced in respective coil sides then the total emf induced will be E1+E10. Similarly, if the emf induced in coil sides 2 and 11 are E2 & E11, then the total emf in coil 2-11 is given as arithmetic sum of E2 and E11.
Thus the total emf at the coil terminal A & B is the phasor sum of (E1+E10), (E2+E11) and (E3+E12). Let us assume (E1+E10) as reference phasor and draw the phasor diagram of the above three emf to get the total emf available at terminal AB.

In the above phasor, ab represents (E1+E10). Since the slots are displaced from each other by angular slot pitch of γ (in our example, it is 20 degree), this means the emf induced in coil 2-11 will be displace by an angle of γ from reference phasor ab. This is shown by ‘bc’ in above phasor. Similarly, ‘cd’ represents the emf induced in coil 3-12 and is displaced by reference phasor by and angle of 2γ.
Thus the total emf across terminals AB of coil will be the phasor sum of ab, bd and cd which is equal to ‘ad’. Let us now calculate this phasor sum.
Since ab, bc and cd are lying in stator slot, therefore their perpendicular bisector must meet at the centre of the circle. Let us now draw perpendicular bisector oe and of on ab and ad respectively as shown in above figure. In general, the angle aob should be equal to angular slot pitch γ, angle aod equal to qγ and angle aof equal to (qγ/2) where q is number of slots per pole per phase.
In right angled triangle aoe,
Sin (γ/2) = ae / oa
ae = oaSin(γ/2)
Thus, ab = 2oaSin(γ/2) as oe is perpendicular bisector of ab.
Therefore, if the coil were concentrated then the emf across coil terminal AB would have been arithmetic sum of emf. This is given as
Emf per coil = Number of slots per pole per phase x 2oeSin(γ/2)
= 2q(oa)Sin(γ/2)
Now, in right angled triangle aof,
Sin(qγ/2) = af / oa
af = (oa)Sin(qγ/2)
Hence the resultant emf ad equal to the phasor sum of ab, bc and cd is given as
ad = 2(oa)Sin(qγ/2)
Therefore as per the definition of distribution factor,
Kd = Phasor Sum of Coil emf / Arithmetic sum of coil emf
= ad / q ab
= [2(oa)Sin(qγ/2)] / [2q(oa)Sin(γ/2)]
= Sin(qγ/2) / qSin(γ/2)
Thus the formula for distribution factor is given as below.

where q is number of slots per pole per phase and γ is angular slot pitch.
Effect of Harmonics on Distribution Factor
In electrical machine, every effort is made to make the magnetic flux density wave sinusoidal in space. But practically, it is never distributed sinusoidally in space. Rather it contains various harmonics. Out of various harmonics, third harmonic is the most dominant. A third harmonic component of flux density wave may be assumed to be produced by 3 poles as compared to the one pole for fundamental component. In view of this, the angular slot pitch for third harmonic will be 3γ and hence nγ for nth harmonics.
Thus the distribution factor for nth harmonics is given as below.
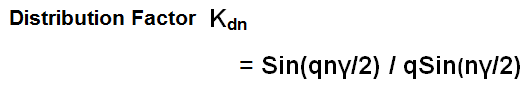
Normally distribution factor for nth harmonics Kdn is less than Kd. This directly means that the emf generated due to nth harmonic component of flux density wave is less than that generated by fundamental component. Thus distribution of armature winding over the slots reduces the harmonics in generated emf and thus making it to approach the sine wave. This is one of the advantages of distributed winding.
Nice and interesting post, keep it up.
I have clearly understood
Thanks for post
Good explanation
Thank you! Kindly share if you like the post.
The result is correct but there’s a typo in… Sin (γ/2) = ae / oe… oe here should be the hypotenuse which is oa
Thank you for pointing the typo.
Good one but we need a number of examples so that the slow learners can grab a point
I’m addicted to this website.
Thank you!Kindly share.