In Transmission Line, two types of capacitance exists: First one is capacitance between the phase conductors and the second one is shunt capacitance between the conductor and the earth. Capacitance between the phase conductors is not only dependent of conductor spacing, radius of conductor and height of conductor from the ground rather it is also influenced by the earth. In this post we will be discussing the effect of Earth on the Capacitance of Transmission Line.
To be straight forward, the effect of earth on the capacitance of lines is to increase it. But it is also important to understand how it happens. In the entire post, I will be trying to prove this. But before we proceed, there are three points which should be kept in mind: a) The electric field lines due to a positive isolated charge emanates from the charge b) Electrical field lines crosses an equipotential surface orthogonally. c) Erath is assumed to be an equipotential conducting infinite plane.
Let us consider an isolated conductor having linear charge density ρ kept at a height of h meter above the ground. As earth is assumed to be equipotential surface, this mean that there must be another imaginary conductor below the earth surface at a depth equal to the height of the conductor as shown in figure below. Also, the charge on this imaginary conductor should be equal but opposite to the actual conductor. This imaginary conductor is called image of the actual conductor and this method is famously known as method of image.
Method of image is basically a way to replace a surface charge distribution with an appropriate charge for the sake of calculation of various parameters viz. potential, electric field etc.
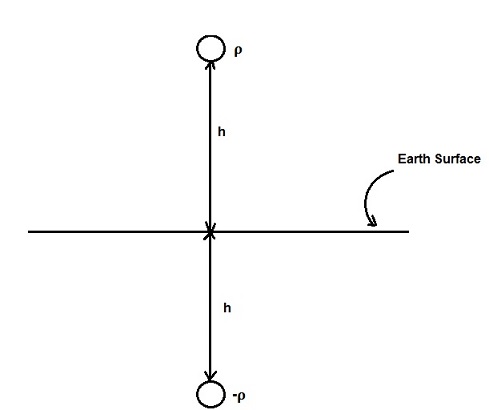
Let us now calculate the capacitance of the above shown isolated conductor to understanding the effect of earth on capacitance. From the above figure, it can be easily seen that the actual conductor with its image is equivalent to single phase transmission line. As we know that the capacitance of single phase transmission line is give as
C = πξ0 / ln(D / r)
Where D = Separation between the Go and Return conductor
r = Radius of conductor
Here in our case, the actual conductor and its image conductors are separated by a distance 2h, hence
Phase to phase Capacitance per unit length
= πξ0 / ln(2h / r) F/m
But this phase to phase capacitance can be assumed to be series connection of phase to ground capacitance of conductors as shown below.
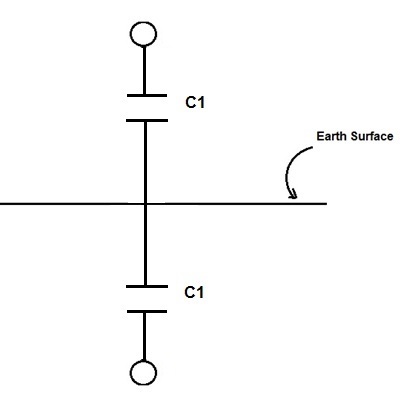
Therefore,
Phase to phase Capacitance = C1/2
C1 = 2πξ0 / ln(2h / r) F/m
From the above value of capacitance, we observe that the capacitance of conductor has increased due to the effect of Earth.
Effect of Earth on Capacitance of Single Phase Transmission Line:
Let us assume that conductor a and b constitute the Go and Return conductor of single phase transmission line. Radius of conductor is assumed to be r. To calculate the effect of earth on the capacitance of single phase transmission line, we need to replace the earth surface charge distribution using method of image. Conductors a’ and b’ are the image conductor of actual conductors a and b respectively.
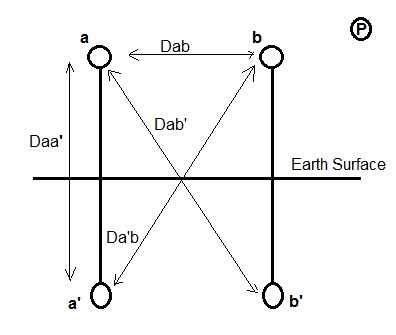
Let P be a point at infinity so that potential at this point is assumed to be zero. Such point is called reference point for the calculation of potential.
Da = Distance of conductor a from point P
Dab = Distance between conductor a and b
Dab’ = Distance between conductor a and b’
Da’b = Distance between conductor a’ and b
We will now calculate the potential Va of conductor a with respect to reference point P.
Va = (ρ/2πξ0)[ln (Da/r) – ln (Da’/Daa’) – ln (Db/Dab) + ln (Db’/ Dab’)]
= (ρ/2πξ0)ln (DabDaa’ / rDab’)
Hence,
ρ / Va = C = 2πξ0 / ln [(Daa’ / Dab’) (Dab / r)]
Thus, the capacitance C of single phase transmission line is given as
C = 2πξ0 / ln [(Daa’ / Dab’) (Dab / r)]
Since Daa’ / Dab’ < 1, therefore from the above expression we can say that the value of capacitance has increased due to the effect of earth. However as the distance of separation between the conductors i.e. Dab is very much small when compared to height of conductor above ground level, therefore for all practical calculation (Daa’ / Dab’) ≈1. Thus the effect of earth on capacitance of transmission line may be neglected.