When the potential difference between the terminals of two or more inductors are same, it is said that they are connected in parallel. As potential difference or voltage across the terminals are same therefore current flowing through the inductors may or may not be same. If the parallel connected inductors have the same value of inductance then equal current will flow through them. If the value of inductance are not same then current through the inductors will be different.
Equivalent Inductance without Magnetic Coupling between Inductors
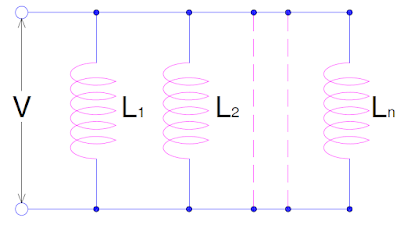
Consider the figure below. In the figure n inductors having inductance of L1, L2,…..,Ln are connected in parallel and a voltage V is applied. Let current I1, I2,….In is flowing through the inductors L1, L2,……Ln.
The emf generated in the inductance will oppose the cause i.e. current flowing through the inductor as per Lenz’s Law. Therefore,
V = L1di1/dt = L2di2/dt = ………=Lndin/dt
But we know that,
I = i1 + i2 +…..+in
Differentiating both side w.r.t time,
dI/dt = di1/dt + di2/dt +…..+din/dt
= V/L1 + V/L2 + ……..+ V/Ln …………….(1)
If the parallel combination of inductors is to be replaced by a single equivalent inductor then,
V = LdI/dt (assuming current I is flowing the equivalent inductor)
dI/dt = V/L …………………(2)
Comparing equation (1) and (2) we get,
V/L = V/L1 + V/L2 + ……..+ V/Ln
1/L = 1/L1 + 1/L2 + …..+ 1/Ln
Thus from the above equation we can find the value of equivalent inductance L. It shall be noted that the above formula is valid if there is no mutual coupling between the inductors. If there exists mutual coupling between the inductors the value of equivalent inductance will depend upon the type of coupling i.e. additive coupling or subtractive coupling. Well, we will consider the two types of coupling and will find the equivalent inductance.
Equivalent Inductance for Additive Mutual Coupling
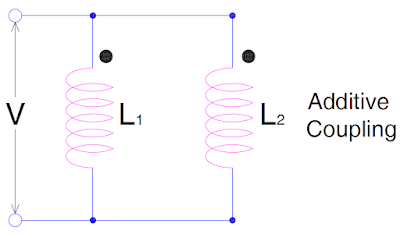
Suppose two inductors with inductance L1 and L2 are connected in parallel as shown in figure below. The coupling between the inductors is assumed to be additive. This additive coupling is shown by two dots on the same side of the inductor in the figure.
Suppose the current flowing through inductor L1 and L2 being i1 and i2 and the mutual inductance is M.
Voltage across L1 and L2 = V
But voltage across L1 = L1di1/dt + Mdi2/dt = V
and across L2 = L2di2/dt + Mdi1/dt = V
Therefore we can write,
L1di1/dt + Mdi2/dt = L2di2/dt + Mdi1/dt
di1/dt (L1 – M) = di2/dt (L2 – M)
di1/dt = [(L2 – M) / (L1 – M)] di2/dt ……………….(1)
Now, the total current flowing i = i1 + i2
Differentiating the above equation w.r.t time we get,
di/dt = di1/dt + di2/dt
= [(L2 – M) / (L1 – M)] di2/dt + di2/dt
= di2/dt [{(L2 – M) / (L1 – M)} + 1]
= di2/dt [(L1+L2-2M) / (L1 – M)] …………………..(2)
Now, if the above combination of inductor is replaced by an equivalent inductor L then
V = Ldi/dt (total current i will flow through the equivalent inductor)
= L x di2/dt [(L1+L2 – 2M) / (L1 – M)] …….. from equation (2)
But V = L2di2/dt + Mdi1/dt
Therefore,
L2di2/dt + Mdi1/dt = L x di2/dt [(L1+L2-2M) / (L1 – M)]
Putting the value of di1/dt from equation (1),
∴ L2di2/dt + M[(L2 – M) / (L1 – M)] di2/dt = L x di2/dt [(L1+L2-2M) / (L1 – M)]
⇒L2 + M[(L2 – M) / (L1 – M)] = L [(L1+L2-2M) / (L1 – M)]
⇒[L2(L1 – M) + M(L2 – M)] / (L1 – M) = L [(L1+L2-2M) / (L1 – M)]
⇒[L2(L1 – M) + M(L2 – M)] = L (L1+L2-2M)
⇒L = [L2(L1 – M) + M(L2 – M)] / (L1+L2-2M)
= (L2L1 – M2) / (L1+L2-2M)
∴Equivalent Inductance L = (L2L1 – M2) / (L1+L2-2M)
Equivalent Inductance for Subtractive Mutual Coupling
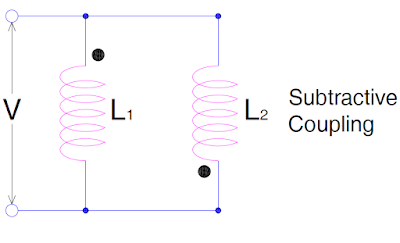
Suppose two inductors with inductance L1 and L2 are connected in parallel as shown in figure below. The coupling between the inductors is assumed to be subtractive. This coupling is shown by two dots on the opposite side of the inductor in the figure.
Suppose the current flowing through inductor L1 and L2 being i1 and i2 and the mutual inductance is M.
Voltage across L1 and L2 = V
But voltage across L1 = L1di1/dt – Mdi2/dt = V
Notice that while finding the emf developed across L1, minus sign is used between L1di1/dt and Mdi2/dt as the coupling between the inductors is subtractive.
and across L2 = L2di2/dt – Mdi1/dt = V
Therefore we can write,
∴ L1di1/dt – Mdi2/dt = L2di2/dt – Mdi1/dt
⇒di1/dt (L1 + M) = di2/dt (L2 + M)
⇒di1/dt = [(L2 + M) / (L1 + M)] di2/dt ……………….(1)
Now, the total current flowing i = i1 + i2
Differentiating the above equation w.r.t time we get,
di/dt = di1/dt + di2/dt
= [(L2 + M) / (L1 + M)] di2/dt + di2/dt
= di2/dt [{(L2 + M) / (L1 + M)} + 1]
= di2/dt [(L1+L2 + 2M) / (L1 + M)] …………………..(2)
Now, if the above combination of inductor is replaced by an equivalent inductor L then
V = Ldi/dt (total current i will flow through the equivalent inductor)
= L x di2/dt [(L1+L2 + 2M) / (L1 + M)] …….. from equation (2)
But V = L2di2/dt + Mdi1/dt
Therefore,
L2di2/dt – Mdi1/dt = L x di2/dt [(L1+L2 + 2M) / (L1 + M)]
Putting the value of di1/dt from equation (1),
L2di2/dt – M[(L2 + M) / (L1 + M)] di2/dt = L x di2/dt [(L1+L2 + 2M) / (L1 + M)]
⇒L2 – M[(L2 + M) / (L1 + M)] = L [(L1+L2 + 2M) / (L1 + M)]
⇒[L2(L1 + M) – M(L2 + M)] / (L1 + M) = L [(L1+L2 + 2M) / (L1 + M)]
⇒[L2(L1 + M) – M(L2 + M)] = L (L1+L2 + 2M)
⇒L = [L2(L1 + M) – M(L2 + M)] / (L1+L2 + 2M)
= (L2L1 – M2) / (L1+L2 + 2M)
∴ Equivalent Inductance L = (L2L1 – M2) / (L1+L2 + 2M)
To summarize,
- Equivalent Inductance L of parallel connected inductors L1, L2, ….,Ln having no mutual coupling among them can be find by using
1/L = 1/L1 + 1/L2 +……..+1/Ln
- If two inductors having inductance L1 and L2 are connected in parallel and the coupling between them is additive, then equivalent inductance L is given as
L = (L2L1 – M2) / (L1+L2 – 2M)
- If two inductors having inductance L1 and L2 are connected in parallel and the coupling between them is subtractive, then equivalent inductance L is given as
L = (L2L1 – M2) / (L1+L2 + 2M)