Symmetrical Fault in Power System refers to kind of fault which leads to short circuit of three phases. This may be either short circuit of three phases or three phases to ground fault. In symmetrical fault, fault currents in phases are symmetrical in the sense that their magnitudes are equal and they are equally displaced by an angle of 120°. Thus, a symmetrical fault may be assumed as a normal case but with high value of current in phases.
Let us consider a symmetrical fault as shown in figure below.
In the figure above, all the three phases i.e. R, Y and B are shorted. This can be assumed as the three lines are connected to a delta connected load with zero impedance in each phase. Taking this assumption, the current in lines will be symmetrical but with higher value. The value of fault current i.e. IR, IY and IB in such fault will only be limited by the source impedance as well as the impedance of line up to the point of fault.
Well, we can analyze such fault by assuming single phase as the condition in other two phases are similar.
Symmetrical Fault in power system is very rare and they rarely take place. But still the study of Symmetrical Fault is important as it is the severe fault and imposes high duty on breaker and equipment.
Calculation of Symmetrical Fault Current
When a short circuit take place at any point in the system, the short circuit current is limited by the system impedance up to the point of fault. Let us assume a fault as shown below.
In the above figure, the impedance up to the point of fault is the sum of impedance of Generator, Transformer and Line. Thus we need to calculate the impedance of each element of system up to the location of fault. As different element of system has different kVA rating therefore per unit or percentage impedance is calculated assuming appropriate kVA rating as base value. Please read Per Unit Value for better understanding.
If the value of per unit or percentage impedance up to the point of fault is X % then short circuit current Isc is given as
Isc = (V / X %)
But percentage impedance X % = 100x( IX / V)
Therefore,
Isc = I (100 / % X)
where I = Full load current
For example, if the percentage impedance up to point of fault is 10% and full load current is 40 A then short circuit current will be [40 x (100 / 10)] = 400 A.
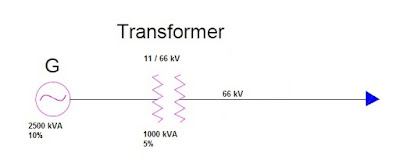
Example: Consider the figure below and calculate the symmetrical fault current considering three phase short circuit at the HV terminal of Transformer. The impedance values are mentioned in the figure.
Solution:
As we need to calculate the short circuit current at the HV terminal of the transformer, therefore first of all we need to calculate the total impedance of the system up to the HV terminal of transformer. But for finding the percentage impedance we need to select a base kVA rating. Well, we choose 1000 kVA as the Base value as calculation with 1000 is quite easier.
% impedance of Generator at Base kVA = (10 / 2500)x1000
= 4 %
% impedance of transformer at base kVA = (5 / 1000)x1000
= 5 %
Thus total impedance up to the point of fault = (5 + 4) %
= 9 %
Now we need to find the full load current at the base kVA at the HV side of transformer.
Full load current I = 1000 / (1.732 x66)
= 8.75 A
Therefore,
Short Circuit current Isc = 8.75x(100 / 9)
= 97.2 A
Calculation of Short Circuit kVA
The product of normal voltage and short circuit current at the point of fault is expressed in Short Circuit kVA even though the voltage at the point of fault reduces to very low value (ideally zero).
Let
V = Normal System Voltage
I = Full load current
% X = % impedance up to the point of fault
Then short circuit current Isc = Ix(100 / %X)
Therefore,
Per phase short circuit VA = V x Isc
= VIx(100 / %X)
Three phase short circuit kVA
= 3VIsc / 1000
= (3VI / 1000) x (100/%X)
= (Base kVA) / (Percentage Impedance)
Thus three phase short circuit kVA is obtained by dividing the Base kVA by percentage impedance.