Travelling wave on transmission line is the voltage / current waves which propagate from the source end to the load end during the transient condition. These waves travel along the line with the velocity equal to velocity of light if line losses are neglected. But practically there always exists some line loss and hence these waves propagate along the line with velocity somewhat lower than the velocity of light.
Concept of Travelling Wave
We know that short transmission line and medium transmission line are studied by their equivalent T or π model. But these models are only useful to study and analyze the steady state response of the line. In case where we are interested in the study of transient behavior, these models are not useful as the line parameters are actually not lumped rather they are non-uniformly distributed over the entire length of the line. For transient analysis, it is very important to consider the line parameters like shunt capacitance and inductance to be distributed and hence their effect must be considered.
Let us consider a lossless transmission line. Let L and C be the inductance and capacitance per unit length of the line.

The above transmission line can be represented by its equivalent circuit having L and C distributed over the whole line as shown below.
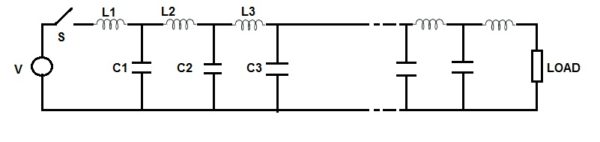
When the switch S is closed, the voltage at the load end does not appear immediately at the load end. As soon as the Switch S is closed, inductance L1 acts as open circuit and capacitance C1 acts as short circuit. Therefore as far as the capacitor C1 is not charged to some value, the charging of C2 through L2 is not possible. This means that charging of C2 through L2 will take some finite time. Similar reasoning applies to the other successive sections. Thus we see that whenever switch S is closed, there is a gradual voltage build up from the source end to the load end over the transmission line. This gradual voltage build up can be thought of due to a voltage wave travelling from one end to the other and the gradual charging of capacitor through inductor is due to current wave.
Let us understand this voltage and current wave in different wave by taking one analogy. Replace the switch S by water valve and each section of inductor and capacitor by a water tank as shown below.
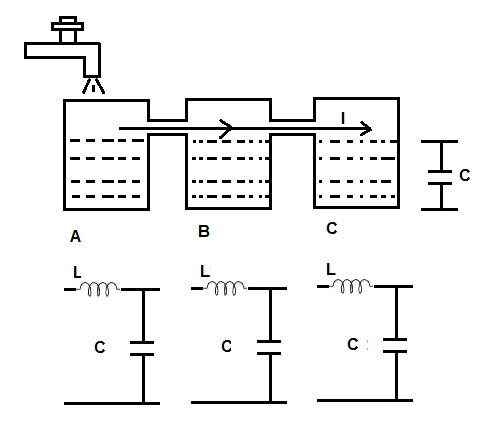
When the water valve is opened, tank A will first fill up to the level of interconnection between the tanks due to flow of water from the valve. This water flow is the flow of current through the inductor L. And the tank level is nothing but the voltage developed across the shunt capacitor C. Once the tank A is filled up, tank B will start filling and when it is also filled up to the level, tank C will start to fill. This means that the filling of tank C will be complete after some finite time and not immediately. Thus the flow of water from tank A to tank C can be assumed as a wave propagating from tank A to tank C. Similarly, the tank levels can also be thought of a wave moving from tank A to tank C. Hope you understood the phenomenon of travelling wave on transmission line by this simple analogy.
Till now, we understood that there are current and voltage wave travelling over the line. Now we want to get the relationship between these two waves.
Relationship between Voltage and Current Wave:
Let the voltage wave and current wave travels a distance x in time t. Therefore the inductance and capacitance of line up to distance x will be Lx and Cx respectively. Let this wave travels a distance dx in time dt.
Since line is assumed to be lossless, whatever is the value of voltage wave and current wave at the beginning, the same will be at any time t. This means that, the magnitude of voltage and current wave at time t will be V and I respectively.
Hence the stored charge in shunt capacitance Q = VCx
and the flux in the series inductance Ø = ILx
But I = dQ/dt
= CVdx/dt
But dx/dt = velocity of travelling wave = ν (say)
Therefore, I = CVν …….(1)
The voltage developed across the shunt capacitance,
V= dØ/dt
=ILdx/dt
= ILν
⇒V = ILν ……….(2)
Dividing equation (1) and (2), we get
V / I = IL / CV
(V/I)2 = L/C
V/I = √(L/C)
The above expression is the ratio of voltage and current having the dimension of impedance. Therefore it is called Surge Impedance. Note that Surge Impedance is the square root of ratio of series inductance L per unit length of line and shunt capacitance C per unit length of line. This simply means that this value will remain constant for a given transmission line. This value will not change due to change in length of line. The value of surge impedance for a typical transmission line is around 400 Ohm and that for a cable is around 40 ohm. Notice that the value of surge impedance for cable is less than that of transmission line. This is due to the higher value of capacitance of cable compared to the transmission line.
Velocity of Travelling Wave:
To get velocity of travelling wave, multiply (1) and (2) as below.
VI = (CVν) x (LIν)
ν2 = 1/LC
ν = √(1/LC) ……..(3)
The above expression is the velocity of travelling wave. Since L and C are per unit values, the velocity of travelling wave is constant. For overhead line the values of L and C are given as
L = 2×10-7ln(d/r) Henry / m
C = 2πε / ln (d/r)
From (3), the velocity of travelling wave for overhead line
ν = 1 / [{2×10-7ln(d/r)}{ 2πε / ln (d/r)}]1/2
= 1/[4πεx10-7]1/2
The permittivity of air, ε = (1/36π) x 10-9
Therefore,
ν = 1 / [4πx(1/36π) x 10-9x10-7]1/2
= 3 x108 m/sec.
From the above expression, we can have following conclusions:
The velocity of travelling wave for a lossless line is equal to the speed of light.
Since the cable core is surrounded by insulations and sheath, its relative permittivity εr >1 and hence ε = ε0εr > ε0 (permittivity of air). Therefore the speed of travelling wave on cable is less than that of transmission line.
Great Content!
Really Insightful for the students.
Didn’t Know That “The velocity of travelling wave for a lossless line is equal to the speed of light”
Good
very well explained. thanks for sharing.