Power Flow Equation through an Inductive Load

Equation of power flow through an inductive load provides the relationship between the sending end voltage, receiving end voltage, line parameters viz. inductance and resistance of line and the impedance angle. The equation is general and can be well applied for Synchronous generator,Synchronous Motor and Transmission Line with slight but appropriate changes. In this post we will be deriving the equation for power flow through an inductive load which is applicable and can be used for synchronous generator as well as transmission line.

Let us assume a transmission line. Let the sending and receiving end voltages are E₁ and E₂ respectively. The line impedance is assumed to be Z. The equivalent circuit of this transmission line (neglecting the shunt capacitance) is shown below.

In the above figure, Source and Load is written instead of sending and receiving end. This is done to illustrate that the figure is applicable for transmission line and synchronous generator. For synchronous generator, sending end will be the source while the receiving end will be the Load. Line impedance will be replaced by synchronous impedance. In this post,bold signs mean their phasor form.

For the flow of current from E₁ to E₂,

E₁ = E₂ + IZ

I = (E₁ – E₂) / Z

   = E₁/Z – E₂/Z ……….(1)

The phasor diagram of the above equivalent circuit will be as shown below.

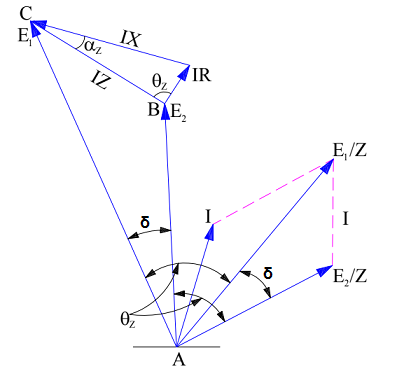
Let us now calculate the active power P₁ at the source (sending end) end E₁ of the impedance. Since active power is equal to multiplication of voltage and component of current in phase with voltage, therefore

Active Power, P1 at source end

= E₁ (Component of I in phase with E₁) ……..(2)

So we need to find the value of current component in phase with source voltage E₁. From (1), it is clear that the line current or armature current (for generator) is difference of two values (E₁/Z) and (E₂/Z). This means, we individually have to find their values and get them subtracted to get the actual value of current I flowing from E₁ to E₂. For this, refer the phasor diagram.

Component of (E₁/Z) along the E1

= (E₁/Z)CosƟ_z

Component of (E₂/Z) along the E1

= (E₂/Z)Cos(δ+Ɵ_z)

From equation (1),

I = [(E₁/Z)CosƟ_z – (E₂/Z)Cos(δ+Ɵ_z)]

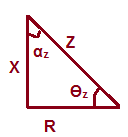
But CosƟ_z = (R/Z) and Ɵ_z = (90 – α_z)

 

Therefore, current I

= [(E₁/Z)CosƟ_z – (E₂/Z)Cos(δ+Ɵ_z)]

= [(E₁R/Z²) – (E₂/Z)Cos{δ+(90 – α_z)}]

= (E₁R/Z²) + (E₂/Z)Sin(δ – α_z)

Now, Active Power P1 at source end from (2)

= (E₁²R/Z²) + (E₁E₂/Z)Sin(δ – α_z) ……(3)

The above expression gives the equation of power flowing from the source or sending end.

The equation for power flowing to the receiving or load end can be derived in the similar fashion. Let us find.

The power P₂ flowing at the load end E₂ through impedance E₂,

P₂ = E₂ (Component of I in phase with E₂)

Component of current I in phase with E₂

= [(E₁/Z)Cos(Ɵ_z – δ) – (E₂/Z)CosƟ_z]

But,

P₂ = E₂ (Component of I in phase with E₂)

     = (E₂E₁/Z)Cos(Ɵ_z – δ) – (E₂²/Z)CosƟ_z

     = (E₂E₁/Z)Cos{90 – (δ+ α_z)} – (E₂²/Z)CosƟ_z

     = (E₂E₁/Z)Sin (δ+ α_z) – (E₂²R/Z²) ……..(4)

The above expression gives the equation for power flow at the load end or receiving end. For power flow through a cylindrical rotor synchronous generator or alternator, E₁ should be replaced by E_f, E₂ by V_t and Z by Z_s. Here, E_f, V_t and Z_s are Excitation Voltage, Armature Terminal Voltage and Synchronous Impedance respectively.

Power input to the Generator will be the power at the source i.e. P₁. Therefore,

Power Input of Generator P_ig from (3),

= (E_f²R/Z²) + (E_fV_t/Z)Sin(δ – α_z)

Since synchronous impedance,

Z_s = r_a + jX_s

So, Power Input of Generator P_ig

= (E_f²r_a/Z_s²) + (E_fV_t/Z_s)Sin(δ – α_z)

Power Output of Generator P_og from (4),

= (E_fV_t/Z_s)Sin(δ+ α_z) – (V_t²r_a/Z_s)

Since the resistance of armature winding is quite low as compared to its inductance, therefore for simplicity this armature resistance r_a may be ignored. Hence Z_s = jX_s and r_a = 0.

Power Output of Generator P_og

= (E_fV_t/X_s)Sin(δ+ α_z)

Since r_a = 0, therefore α_z = 0 as can be seen from impedance triangle.

Power Output of Generator P_og

= (E_fV_t/X_s)Sinδ

You must be very much familiar with the above power equation of the generator. This is very useful equation and we draw power angle curve of generator using the above equation. Note that angle δ is the angle between excitation emf E_f and terminal voltage V_t, hence it is load angle for generator.